Part I: Propositional Logic
7. “Or”
7.1 A historical example: The Euthryphro argument
The philosopher Plato (who lived from approximately 427 BC to 347 BC) wrote a series of great philosophical texts. Plato was the first philosopher to deploy argument in a vigorous and consistent way, and in so doing he showed how philosophy takes logic as its essential method. We think of Plato as the principal founder of Western philosophy. The American philosopher Alfred Whitehead (1861-1947) in fact once famously quipped that philosophy is a “series of footnotes to Plato”.
Plato’s teacher was Socrates (c. 469-399 B.C.), a gadfly of ancient Athens who made many enemies by showing people how little they knew. Socrates did not write anything, but most of Plato’s writings are dialogues, which are like small plays, in which Socrates is the protagonist of the philosophical drama that ensues. Several of the dialogues are named after the person who will be seen arguing with Socrates. In the dialogue Euthyphro, Socrates is standing in line, awaiting his trial. He has been accused of corrupting the youth of Athens. A trial in ancient Athens was essentially a debate before the assembled citizen men of the city. Before Socrates in line is a young man, Euthyphro. Socrates asks Euthyphro what his business is that day, and Euthyphro proudly proclaims he is there to charge his own father with murder. Socrates is shocked. In ancient Athens, respect for one’s father was highly valued and expected. Socrates, with characteristic sarcasm, tells Euthyphro that he must be very wise to be so confident. Here are two profound and conflicting duties: to respect one’s father, and to punish murder. Euthyphro seems to find it very easy to decide which is the greater duty. Euthyphro is not bothered. To him, these ethical matters are simple: one should be pious. When Socrates demands a definition of piety that applies to all pious acts, Euthyphro says,
Piety is that which is loved by the gods and impiety is that which is not loved by them.
Socrates observes that this is ambiguous. It could mean, an act is good because the gods love that act. Or it could mean, the gods love an act because it is good. We have, then, an “or” statement, which logicians call a “disjunction”:
Either an act is good because the gods love that act, or the gods love an act because it is good.
Might the former be true? This view—that an act is good because the gods love it—is now called “divine command theory”, and theists have disagreed since Socrates’s time about whether it is true. But, Socrates finds it absurd. For, if tomorrow the gods love, say, murder, then, tomorrow murder would be good.
Euthyphro comes to agree that it cannot be that an act is good because the gods love that act. Our argument so far has this form:
Either an act is good because the gods love that act, or the gods love an act because it is good.
It is not the case that an act is good because the gods love it.
Socrates concludes that the gods love an act because it is good.
Either an act is good because the gods love that act, or the gods love an act because it is good.
It is not the case that an act is good because the gods love it.
_____
The gods love an act because it is good.
This argument is one of the most important arguments in philosophy. Most philosophers consider some version of this argument both valid and sound. Some who disagree with it bite the bullet and claim that if tomorrow God (most theistic philosophers alive today are monotheists) loved puppy torture, adultery, random acts of cruelty, pollution, and lying, these would all be good things. (If you are inclined to say, “That is not fair, God would never love those things”, then you have already agreed with Socrates. For, the reason you believe that God would never love these kinds of acts is because these kinds of acts are bad. But then, being bad or good is something independent of the love of God.) But most philosophers agree with Socrates: they find it absurd to believe that random acts of cruelty and other such acts could be good. There is something inherently bad to these acts, they believe. The importance of the Euthyphro argument is not that it helps illustrate that divine command theory is an enormously strange and costly position to hold (though that is an important outcome), but rather that the argument shows ethics can be studied independently of theology. For, if there is something about acts that makes them good or bad independently of a god’s will, then we do not have to study a god’s will to study what makes those acts good or bad.
Of course, many philosophers are atheists so they already believed this, but for most of philosophy’s history, one was obliged to be a theist. Even today, lay people tend to think of ethics as an extension of religion. Philosophers believe instead that ethics is its own field of study. The Euthyphro argument explains why, even if you are a theist, you can study ethics independently of studying theology.
But is Socrates’s argument valid? Is it sound?
7.2 The disjunction
We want to extend our language so that it can represent sentences that contain an “or”. Sentences like
Tom will go to Berlin or Paris.
We have coffee or tea.
This web page contains the phrase “Mark Twain” or “Samuel Clemens.”
Logicians call these kinds of sentences “disjunctions”. Each of the two parts of a disjunction is called a “disjunct”. The idea is that these are really equivalent to the following sentences:
Tom will go to Berlin or Tom will go to Paris.
We have coffee or we have tea.
This web page contains the phrase “Mark Twain” or this web page contains the phrase “Samuel Clemens.”
We can, therefore, see that (at least in many sentences) the “or” operates as a connective between two sentences.
It is traditional to use the symbol “v” for “or”. This comes from the Latin “vel,” meaning (in some contexts) or.
The syntax for the disjunction is very basic. If Φ and Ψ are sentences, then
(Φ v Ψ)
is a sentence.
The semantics is a little more controversial. This much of the defining truth table, most people find obvious:
| Φ | Ψ | (ΦvΨ) |
|---|---|---|
| T | T | |
| T | F | T |
| F | T | T |
| F | F | F |
Consider: if I promise that I will bring you roses or lilacs, then it seems that I told the truth either if I have brought you roses but not lilacs, or if I brought you lilacs but not roses. Similarly, the last row should be intuitive, also. If I promise I will bring you roses or lilacs, and I bring you nothing, then I spoke falsely.
What about the first row? Many people who are not logicians want it to be the case that we define this condition as false. The resulting meaning would correspond to what is sometimes called the “exclusive ‘or’”. Logicians disagree. They favor the definition where a disjunction is true if its two parts are true; this is sometimes called the “inclusive ‘or’”. Of course, all that matters is that we pick a definition and stick with it, but we can offer some reasons why the “inclusive ‘or’”, as we call it, is more general than the “exclusive ‘or’”.
Consider the first two sentences above. It seems that the first sentence—“Tom will go to Berlin or Paris”—should be true if Tom goes to both. Or consider the second sentence, “We have coffee or tea.” In most restaurants, this means they have both coffee and they have tea, but they expect that you will order only one of these. After all, it would be strange to be told that they have coffee or tea, and then be told that it is false that they have both coffee and tea. Or, similarly, suppose the waiter said, “We have coffee or tea”, and then you said “I’ll have both”, and the waiter replied “We don’t have both”. This would seem strange. But if you find it strange, then you implicitly agree that the disjunction should be interpreted as the inclusive “or”.
Examples like these suggest to logicians that the inclusive “or” (where the first row of the table is true) is the default case, and that the context of our speech tells us when not both disjuncts are true. For example, when a restaurant has a fixed price menu—where you pay one fee and then get either steak or lobster—it is understood by the context that this means you can have one or the other but not both. But that is not logic, that is social custom. One must know about restaurants to determine this.
Thus, it is customary to define the semantics of the disjunction as
| Φ | Ψ | (ΦvΨ) |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
We haven’t lost the ability to express the exclusive “or”. We can say, “one or the other but not both”, which is expressed by the formula “((Φ v Ψ) ^ ¬(Φ ^ Ψ))”. To check, we can make the truth table for this complex expression:
| Φ | Ψ | (Φ ^ Ψ) | (Φ v Ψ) | ¬(Φ ^ Ψ) | ((Φ v Ψ) ^ ¬(Φ ^ Ψ)) |
|---|---|---|---|---|---|
| T | T | T | T | F | F |
| T | F | F | T | T | T |
| F | T | F | T | T | T |
| F | F | F | F | T | F |
Note that this formula is equivalent to the exclusive “or” (it is true when Φ is true or Ψ is true, but not when both are true or both are false). So, if we need to say something like the exclusive “or”, we can do so.
7.3 Alternative forms
There do not seem to be many alternative expressions in English equivalent to the “or”. We have
P or Q
Either P or Q
These are both expressed in our logic with (P v Q).
One expression that does arise in English is “neither…nor…”. This expression seems best captured by simply making it into “not either… or…”. Let’s test this proposal. Consider the sentence
Neither Smith nor Jones will go to London.
This sentence expresses the idea that Smith will not go to London, and that Jones will not go to London. So, it would surely be a mistake to express it as
Either Smith will not go to London or Jones will not go to London.
Why? Because this latter sentence would be true if one of them went to London and one of them did not. Consider the truth table for this expression to see this. Use the following translation key.
P: Smith will go to London.
Q: Jones will go to London.
Then suppose we did (wrongly) translate “Neither Smith nor Jones will go to London” with
(¬P v ¬Q)
Here is the truth table for this expression.
| P | Q | ¬Q | ¬P | (¬Pv¬Q) |
|---|---|---|---|---|
| T | T | F | F | F |
| T | F | T | F | T |
| F | T | F | T | T |
| F | F | T | T | T |
Note that this sentence is true if P is true and Q is false, or if Q is true and P is false. In other words, it is true if one of the two goes to London. That’s not what we mean in English by that sentence claiming that neither of them will go to London.
The better translation is ¬(PvQ).
| P | Q | (PvQ) | ¬(PvQ) |
|---|---|---|---|
| T | T | T | F |
| T | F | T | F |
| F | T | T | F |
| F | F | F | T |
This captures the idea well: it is only true if each does not go to London. So, we can simply translate “neither…nor…” as “It is not the case that either… or…”.
7.4 Reasoning with disjunctions
How shall we reason with the disjunction? Looking at the truth table that defines the disjunction, we find that we do not know much if we are told that, say, (P v Q). P could be true, or it could be false. The same is so for Q. All we know is that they cannot both be false.
This does suggest a reasonable and useful kind of inference rule. If we have a disjunction, and we discover that half of it is false, then we know that the other half must be true. This is true for either disjunct. This means we have two rules, but we can group together both rules with a single name and treat them as one rule:
(Φ v Ψ)
¬Φ
_____
Ψ
and
(Φ v Ψ)
¬Ψ
_____
Φ
This rule is traditionally called “modus tollendo ponens”.
What if we are required to show a disjunction? One insight we can use is that if some sentence is true, then any disjunction that contains it is true. This is so whether the sentence makes up the first or second disjunct. Again, then, we would have two rules, which we can group together under one name:
Φ
_____
(Φ v Ψ)
and
Ψ
_____
(Φ v Ψ)
This rule is often called “addition”.
The addition rule often confuses students. It seems to be a cheat, as if we are getting away with something for free. But a moment of reflection will help clarify that just the opposite is true. We lose information when we use the addition rule. If you ask me where John is, and I say, “John is in New York”, I told you more than if I answered you, “John is either in New York or in New Jersey”. Just so, when we go from some sentence P to (PvQ), we did not get something for free.
This rule does have the seemingly odd consequence that from, say, 2+2=4 you can derive that either 2+2=4 or 7=0. But that only seems odd because in normal speech, we have a number of implicit rules. The philosopher Paul Grice (1913-1988) described some of these rules, and we sometimes call the rules he described “Grice’s Maxims”.[9] He observed that in conversation we expect people to give all the information required but not more; to try to be truthful; to say things that are relevant; and to be clear and brief and orderly. So, in normal English conversations, if someone says, “Tom is in New York or New Jersey,” they would be breaking the rule to give enough information, and to say what is relevant, if they knew that Tom was in New York. This also means that we expect people to use a disjunction when they have reason to believe that either or both disjuncts could be true. But our logical language is designed only to be precise, and we have been making the language precise by specifying when a sentence is true or false, and by specifying the relations between sentences in terms of their truth values. We are thus not representing, and not putting into our language, Grice’s maxims of conversation. It remains true that if you knew Tom is in New York, but answered my question “Where is Tom?” by saying “Tom is in New York or New Jersey”, then you have wasted my time. But you did not say something false.
We are now in a position to test Socrates’s argument. Using the following translation key, we can translate the argument into symbolic form.
P: An act is good because the gods love that act.
Q: The gods love an act because it is good.
Euthyphro had argued
![Rendered by QuickLaTeX.com \[ \fitchprf{\pline[1.]{(P \lor Q)}[premise]} { } \]](https://milnepublishing.geneseo.edu/app/uploads/quicklatex/quicklatex.com-0070cd4d0d96e32d5b62490d8660092f_l3.png)
Socrates had got Euthryphro to admit that
![Rendered by QuickLaTeX.com \[ \fitchprf{ \pline[1.]{(P \lor Q)}[premise]\\ \pline[2.]{\lnot P}[premise] } { } \]](https://milnepublishing.geneseo.edu/app/uploads/quicklatex/quicklatex.com-8117d4e4a3e05f28610622e3c2496b43_l3.png)
And so we have a simple direct derivation:
![Rendered by QuickLaTeX.com \[ \fitchprf{ \pline[1.]{(P \lor Q)}[premise]\\ \pline[2.]{\lnot P}[premise] } { \pline[3.]{Q}[modus tollendo ponens, 1, 2] } \]](https://milnepublishing.geneseo.edu/app/uploads/quicklatex/quicklatex.com-5ef082e2b9b94728ef0ecaa57c0db84f_l3.png)
Socrates’s argument is valid. I will leave it up to you to determine whether Socrates’s argument is sound.
Another example might be helpful. Here is an argument in our logical language.
(P v Q)
¬P
(¬P → (Q → R))
_____
(R v S)
This will make use of the addition rule, and so is useful to illustrating that rule’s application. Here is one possible proof.
![Rendered by QuickLaTeX.com \[ \fitchprf{ \pline[1.]{(P \lor Q)}[premise]\\ \pline[2.]{\lnot P}[premise]\\ \pline[3.]{(\lnot P \lif (Q \lif R))}[premise] } { \pline[4.]{Q}[modus tollendo ponens, 1, 2]\\ \pline[5.]{(Q \lif R)}[modus ponens, 3, 2]\\ \pline[6.]{R}[modus ponens, 5, 4]\\ \pline[7.]{(R \lor S)}[addition, 6] } \]](https://milnepublishing.geneseo.edu/app/uploads/quicklatex/quicklatex.com-524192adbaecff8423be58987901798b_l3.png)
7.5 Alternative symbolizations of disjunction
We are fortunate that there have been no popular alternatives to the use of “v” as a symbol for disjunction. Perhaps the second most widely used alternative symbol was “||”, such that (P v Q) would be symbolized:
(P || Q)
7.6 Problems
- Prove the following using a derivation.
- Premises: (PvQ), (Q → S), (¬S^T). Conclusion: (T^P).
- Premises: ((P → ¬Q) ^ (R → S)), (Q v R). Conclusion: (P → S).
- Premises: ((P^Q) v R), ((P^Q) → S), ¬S. Conclusion: R.
- Premises: (RvS), ((S → T) ^ V), ¬T, ((R^V) → P). Conclusion: (PvQ).
- Premises: ((P → Q) v (¬R → S)), ((P → Q) → T), (¬T ^ ¬S). Conclusion: (R v V).
- Premises: (P v S), (T → ¬S), T. Conclusion: ((P v Q) v R).
- Conclusion: (P → (PvQ)).
- Conclusion: ((PvQ) → (¬P → Q)).
- Conclusion: ((PvQ) → (¬Q → P)).
- Conclusion: (((PvQ) ^ (¬Q v ¬R)) → (R → P)).
- Consider the following four cards in figure 7.1. Each card has a letter on one side, and a shape on the other side.
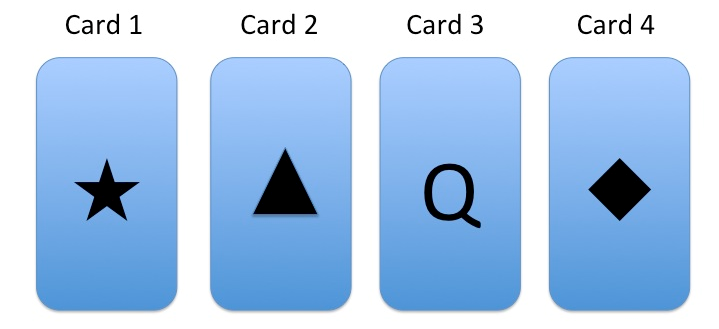
For each of the following claims, determine (1) the minimum number of cards you must turn over to check the claim, and (2) what those cards are, in order to determine if the claim is true of all four cards.
- If there is a P or Q on the letter side of the card, then there is a diamond on the shape side of the card.
- If there is a Q on the letter side of the card, then there is either a diamond or a star on the shape side of the card.
- In normal colloquial English, write your own valid argument with at least two premises, at least one of which is a disjunction. Your argument should just be a paragraph (not an ordered list of sentences or anything else that looks like formal logic). Translate it into propositional logic and prove it is valid.
- Translate the following passage into our propositional logic. Prove the argument is valid.
Either Dr. Kronecker or Bishop Berkeley killed Colonel Cardinality. If Dr. Kronecker killed Colonel Cardinality, then Dr. Kronecker was in the kitchen. If Bishop Berkeley killed Colonel Cardinality, then he was in the drawing room. If Bishop Berkeley was in the drawing room, then he was wearing boots. But Bishop Berkeley was not wearing boots. So, Dr. Kronecker killed the Colonel.
- Translate the following passage into our propositional logic. Prove the argument is valid.
Either Wittgenstein or Meinong stole the diamonds. If Meinong stole the diamonds, then he was in the billiards room. But if Meinong was in the library, then he was not in the billiards room. Therefore, if Meinong was in the library, Wittgenstein stole the diamonds.
[9] Grice (1975).

