15. Relations, functions, identity, and multiple quantifiers

15.1  Relations

We have developed a first order logic that is sufficient to describe many things.  The goal of this chapter is to discuss ways to extend and apply this logic.  We will introduce relations and functions, make some interesting observations about identity, and discuss how to use multiple quantifiers.

Recall that if we have a predicate of arity greater than one, we sometimes call that a “relation”.  An arity one predicate like “… is tall” does not relate things in our domain of discourse.  Rather, it tells us about a property of a thing in our domain of discourse.  But an arity two predicate like “… is taller than …” relates pairs of things in our domain of discourse.

More generally, we can think of a relation as a set of ordered things from our domain of discourse.  An arity two relation is thus a collection of ordered pairs of things; the relation “…is taller than…” would be all the ordered pairs of things where the first is taller than the second.  The predicate “… is taller than…” would be true of all these things.  The relation “… sits between … and …” would be the collection of all the triples of things where the first sat between the second and third.  The predicate “… sits between … and …” would be true of all of these things.

Logicians have developed a host of useful ways of talking about relations, especially relations between just two things.  We can illustrate this with an example.  Hospitals and other medical treatment facilities often need blood for transfusions.  But not any kind of blood can do.  One way to classify kinds of blood is using the ABO system.  This divides kinds of blood into four groups:  A, B, AB, and O.  This classification describes antigens on the surface of the blood cells.  It is a very useful classification, because some people have an immune system that will not tolerate the antigens on other kinds of blood.  This tolerance is determined by one’s blood group.

Those with type O blood can give blood to anyone, without causing an immune reaction.  Those with type A can give blood to those with type A and type AB.  Those with type B can give blood to those with type B and type AB.  And those with type AB can only give to type AB.  Let arrows mean, can be given to people with this blood type without causing an allergic reaction in the following diagram:
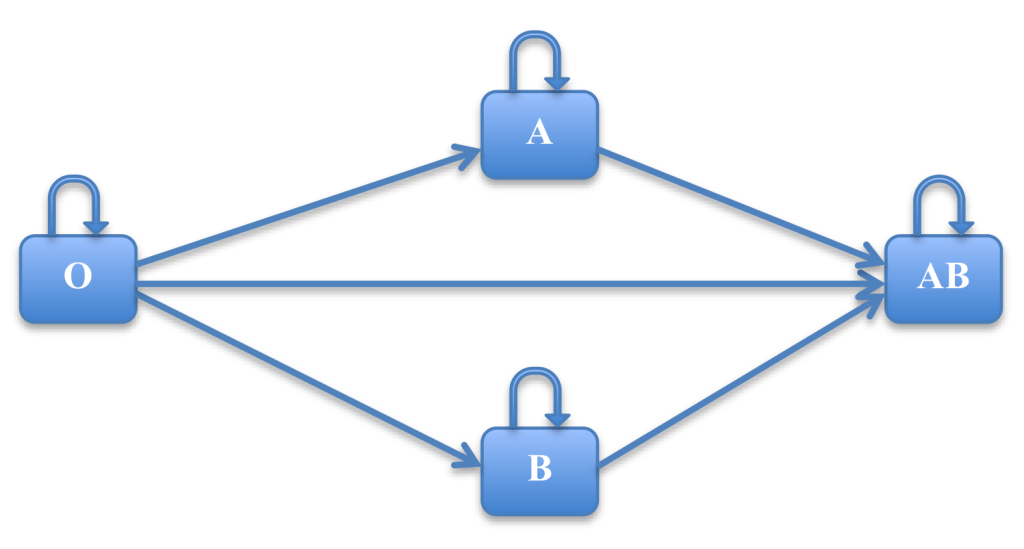Notice a number of things.  First, every blood type can share blood with people of that blood type.  But it is not always the case that if I can share blood with you, you can share blood with me:  it could be that I am type O and you are type B.  Also, if I can share blood with you, and you can share blood with Tom, then I can share blood with Tom.

The first feature of relations is called “reflexive”.  For any relation Φ(xy), the relation is reflexive if and only if:

∀xΦ(xx)

Examples of reflexive relations in English include “…is as old as…”.  Each person is as old as herself.  A relation that is not reflexive is, “…is older than …”.  No person is older than herself.

For any relation Φ, the relation is symmetric if and only if:

∀x∀y(Φ(x y) → Φ(y x))

Examples of symmetric relations in English include “…is married to…”.  In our legal system at least, if Pat is married to Chris, then Chris is married to Pat.

Finally, call a relation “transitive” if and only if

∀x∀y∀z((Φ(x y)^Φ(y z)) → Φ(x z))

Examples of transitive relations in English include “…is older than…”.  If Tom is older than Steve, and Steve is older than Pat, then Tom is older than Pat.

Return now to our example of blood types.  We introduce the following translation key:

Gxy:  x can give blood to y without causing an immune reaction

It is the case that

∀xGxx

And so we know that the relation G is reflexive.  A person with type O blood can give blood to himself, a person with type AB blood can give blood to herself, and so on.  (People do this when they store blood before a surgery.)  Is the relation symmetric?  Consider whether the following is true:

∀x∀y(Gxy → Gyx)

A moment’s reflection reveals this isn’t true.  A person of type O can give blood to a person of type AB, but the person with type AB blood cannot give blood to the person with type O, without potentially causing a reaction.  So G is not symmetric.

Finally, to determine if G is transitive, consider whether the following is true.

∀x∀y∀z((Gxy ^ Gyz) → Gxz)

A person with type O blood can give blood to a person with type A blood, and that person can give blood to someone of type AB.  Does it follow that the person with type O can give blood to the person with AB?  It does.  And similarly this is so for all other possible cases.  G is a transitive relation.

15.2  Functions

A function is a kind of relation between two or more things.  What all functions have in common is that they relate some specific number of things to precisely one thing. A familiar example from mathematics might be the squaring function.  We write for this, n2.  This takes one number, say 7, and then relates it to exactly one other number, 49.  Or addition is a function that takes two numbers and relates them to exactly one other number, their sum.

The idea of a function is very general, and extends beyond mathematics.  For example, each of the following could be a function (if certain things are assumed beforehand):

the mother of…

the father of…

Think of how you could use something like this in our logical language.  You could say, “The father of Tom is Canadian”.  But now, who is Canadian?  Not Tom.  Tom’s father is.  In this sentence, “the father of…” acts as a function.  It relates a person to another person. And, in our predicate, “the father of Tom” acts like a name, in that it refers to one thing.

Functions have an arity.  Addition is an arity two function; it takes two objects in order to form a symbolic term.  But in order to be a function, the resulting symbolic term must always refer to only one object.  (This rule gets broken a lot in mathematics, where some relations are called “functions” but can have more than one output.  This arises because in circumscribed domains of discourse, those operations are functions, and then they get applied in new domains but are still called “functions”.  Thus, the square root function is a function when we are studying the natural numbers, but once we introduce negative numbers it no longer is a function.  But mathematicians call it a “function” because it is in limited domains a function, and because the diverse output is predictable in various ways.  Logic is the only field where one earns the right to call mathematicians sloppy.)

Functions are surprisingly useful.  Computers, for example, can be understood as function machines, and programming can be usefully described as the writing of functions for the computer.  Much of mathematics is concerned with studying functions, and they often prove useful for studying other things in mathematics that are not themselves functions.

We can add functions to our logical language.  We will let f, g, h, … be functions.  Each function, as noted, has an arity.  A function of arity n combined with n symbolic terms is a symbolic term.

Thus, to make a key to translate the sentence above, we can have:

Kx:  x is Canadian.

fx:  the father of x.

a:  Tom

b:  Steve

(Obviously, we are assuming that each person has only one father.  Arguably that is only one use of the word “father,” but our goal here is to create a familiar example, not to take sides in any issue about family relations.  So we will allow the assumption just to make our point.)  Using that key, the following would mean “Tom is Canadian”:

Ka

And the following would mean “The father of Tom is Canadian”:

Kfa

We can also say something like, “Tom’s paternal grandfather is Canadian”:

Kffa

Or even, “Tom’s paternal great-grandfather is Canadian”:

Kfffa

That works because the father of the father of Tom is the paternal grandfather of Tom, which then is a symbolic term, and we can apply the function to it.  Recall that, when a rule can be applied repeatedly to its product, we call this “recursion”.

15.3  Identity

There is one predicate that has always been enormously useful, and which in most logical systems is singled out for special attention.  This is identity.

In English, the word “is” is multiply ambiguous, and we must sort out identity from predication and existence.  For example, consider the following sentences:

Malcolm X is a great orator.

Malcolm X is Malcolm Little.

Malcolm X is.

The last example is not very common in English usage, but it is grammatical.  Here we see the “is” of existence.  The sentence asserts that Malcolm X exists.  In the first sentence, we would treat “…is a great orator” as an arity one predicate.  The “is” is part of the predicate, and in our logic, cannot be distinguished from the predicate.  But the second case uses the “is” of identity.  It asserts that Malcolm X and Malcolm Little are the same thing.

Because it is so common to use the symbol “=” for identity, we will use it, also.  Strictly speaking, our syntax requires prefix notation.  But for any language we create, we could introduce an arity two predicate

Ixy:  x is identical to y

And then we could say, whenever we write “α=β” we really mean “Iαβ”.

Note identity describes a relation that is reflexive, symmetric, and transitive.  Everything is identical to itself.  If a=b then b=a.  And if a=b and b=c then a=c.

One special feature of identity is that we know that if two things are identical, then anything true of one is true of the other.  In fact, the philosopher Leibniz defined identity with a principle that we call Leibniz’s Law:  a and b are identical if and only if they have all and only the same properties.  Our logic must take identity as a primitive, however, because we have no way in our logic of saying “all properties” (this is what “first order” in “first order logic” means:  our quantifiers have only particular objects in their domain).

Leibniz’s insight, however, suggests an inference rule.  If α and β are symbolic terms, and Φ(α) means that Φ is a formula in which α appears, we can say

Φ(α)

α=β

_____

Φ(β)

Where we replace one or more occurrences of α in Φ with β.  We can call this rule, “indiscernibility of identicals”.  We sometimes also call this, “substitution of identicals”.

This is an interesting kind of rule.  Some logicians would call this a “non-logical rule”.  The reason is, we know it is proper because we know the meaning of “=”.  Unlike, for example, modus ponens, which identifies a logical relation between two kinds of sentences, this rule relies not on the semantics of a connective, but rather on the meaning of a predicate.  This notion of “non-logical” is a term of art, but it does seem profound.  Adding such rules to our language can strengthen it considerably.

Adding identity to our language will allow us to translate some expressions that we would be unable to translate otherwise.  Consider our example above, for functions.  How would we translate the expression, “Steve is the father of Tom”?  We could add to our language a predicate, “… is the father of …”.  However, it is interesting that in this expression (“Steve is the father of Tom”), the “is” is identity.  A better translation (using the key above) would be:

b=fa

We can also say things like, “The father of Steve is the paternal grandfather of Tom”:

fb=ffa

Consider now a sentence like this:  someone is the father of Tom.  Again, if we had a predicate for “… is the father of …”, we could just say, there is something that is the father of Tom.  But given that we have a function for “the father of x” we could also translate this phrase as:

∃x  x=fa

We can see from these examples that there are interesting parallels between relations (including functions) and predicates.  To represent some kind of function, we can introduce a function into our language, which acts as a special kind of symbolic term, but it is also possible to identify a predicate that is true of all and only those things that the function relates.  Nonetheless, we must be careful to distinguish between predicates, which when combined with the appropriate number of names form a sentence; and functions, which when combined with the appropriate number of other terms are symbolic terms.  In our logic, treating predicates like functions (that is, taking them as symbolic terms for other predicates) will create nonsense.

Finally, we had as an example above, the sentence “Malcolm X is”.  This is equivalent to “Malcolm X exists”.   Let c mean Malcolm X.  Identity allows us to express this sentence. We say that there is at least one thing that is Malcolm X:

∃x  x=c

15.4  Examples using multiple quantifiers

We have only just begun to explore the power of quantifiers.  Consider now the following sentences:

Every number is greater than or equal to some number.

Some number is greater than or equal to every number.

Every number is less than or equal to some number.

Some number is less than or equal to every number.

Depending upon our domain of discourse, some of these sentences are true, and some of them are false.  Can we represent them in our logical language?

Suppose that we introduce an arity two predicate for “greater than or equal to”:

Gxy:  x is greater than or equal to y

We can follow tradition, and use “≥”.  Thus, when we write “α≥β” we understand that this is “Gαβ”.  Let us also assume that our domain of discourse is the natural numbers.  That is, we are talking only about 1, 2, 3, 4….

We can see now how to take a first step toward expressing these sentences.  If we write:

x≥y

We have said that x is greater than or equal to y.  We have used quantifiers to say “all”, and we can write

∀x x≥y

Which says that every number is greater than or equal to y.  But how will we capture the sentences above?  We will need to use multiple quantifiers.  To say that “every number is greater than some number”, we will write

∀x∃y x≥y

This raises important questions about how to interpret multiple quantifiers.  Using multiple quantifiers expands the power of our language enormously.  However, we must be very careful to understand their meaning.

Consider the following two sentences, which will use our key above.

∀x∃y x≥y

∃y∀x x≥y

Do they have the same meaning?

As we understand the semantics of quantifiers, we will say that they do not.  The basic idea is that we read the quantifiers from left to right.  Thus, the first sentence above should be translated to English as “Every number is greater than or equal to some number”.  The second sentence should be translated, “Some number is less than or equal to every number”.  They have very different meanings.  Depending upon our domain of discourse, they could have different truth values.  For example, if we use the natural numbers as our domain of discourse, the first sentence is true and the second sentence is true.  However, if we used the integers for our domain of discourse, so that we included negative numbers, then the first sentence is true but the second sentence is false.

It may be helpful to think of multiple quantifiers in the following way.  If we were to instantiate the quantifiers, then, we would work from left to right.  Thus, the first sentence says something like, pick any number in our domain of discourse, then there will be at least one number in our domain of discourse that is less than or equal to that first number that you already picked.  The second sentence says something quite different:  there is at least one number in our domain of discourse such that, if you pick that number, then any number in our domain of discourse is greater than or equal to it.

With this in mind, we are now able to translate the four phrases above.  We include the English with the translation to avoid any confusion.

Every number is greater than or equal to some number.

∀x∃y x≥y

Some number is greater than or equal to every number.

∃x∀y x≥y

Every number is less than or equal to some number.

∀x∃y y≥x

Some number is less than or equal to every number.

∃x∀y y≥x

As we noted above, the truth value of these sentences can change if we change our domain of discourse.  If our domain of discourse is the natural numbers, then only the second sentence is false; this is because for the natural numbers there is a least number (1), but there is no greatest number.  But if our domain of discourse is the integers, then the second and fourth sentences are false.  This is because with the negative numbers, there is no least number:  you can always find a lesser negative number.

Hopefully it becomes very clear now why we need the possibility of a number of variables for our quantifiers.  We could not write the expressions above if we did not have discernibly distinct variables to allow different quantifiers to bind different locations in the predicate.

15.5  Capturing specific quantities

It can be interesting to see a powerful use of multiple quantifiers.  In 1905, the British philosopher Bertrand Russell (1872-1970) published a very insightful and influential paper, “On Denoting”.  This paper, and additional work by Russell that followed it, made brilliant use of a series of problems in logic and language that perplexed Russell.  Russell was concerned about a number of puzzles that arise around phrases like, “The current President of the United States…”.  Such a phrase seems to act like a name, and yet a number of strange outcomes arise if we treat it as a name.

First, suppose we say

It is not the case that Sam is bald.

Now suppose that anyone who is not bald has hair.  Then, we could reason that:

Sam has hair.

That seems correct, if we grant the premise that all those who are not bald have hair.  But now consider the following sentence.

It is not the case that the present King of France is bald.

By the same reasoning, this would seem to entail that:

The present King of France has hair.

But that’s not right.  There is no present King of France!

It gets worse.  Let us assert that

The present King of France does not exist.

This seems to pick out a thing, the present King of France, and ascribe to it a property, not existing.  After all, in our logical language, each name must refer to something.  But if we can pick out that thing in order to describe it as not existing, does it not exist?  That is, is there not a thing to which the term refers?

Some philosophers indeed argued that every term, even in a natural language, must have a thing that it refers to.  The philosopher Alexius Meinong (1853-1920), for example, proposed that every name has a referent that has being, but that existence was reserved for particular actual objects.  This is very strange, when you consider it:  it means that “the round square” refers to something, a something that has being, but that lacks existence.  Russell thought this a terrible solution, and wanted to find another.

Russell uses a different example to illustrate a third problem.  Suppose that

George IV wished to know whether Scott was the author of Waverley.

Here Russell raises a problem related to one that the mathematician Gottlob Frege had already observed.  Namely, if Scott=the author of Waverley, then one might suppose that we could substitute “Scott” where we see “the author of Waverley” and get a sentence that has the same truth value.  That is, we introduced above a rule—indiscernibility of identicals—that, if applied here, should allow us to replace “the author of Waverley” with “Scott” if Scott=the author of Waverley.  But that fails:  it is not the case that

George IV wished to know whether Scott was Scott.

George IV already knows that Scott is Scott.

Russell put forward a brilliant solution to these puzzles.  He developed an analysis of some English phrases into a logical form that is rather different than we might expect.  For example, he argues the proper form to translate “It is not the case that the present King of France is bald” is something like this.  Let “Gx” mean “x is the present king of France” and “Hx” mean “x is bald”, then this sentence is translated:

∃x((Gx ^ Hx) ^ ∀y(Gy → x=y))

This says there is something—call it x for now—that is the present king of France, and that thing is bald, and if anything is the present king of France it is identical to x.  This second clause is a way of saying that there is only one king of France, which is how Russell captures the meaning of “the” in “the present king of France”.

This sentence is false, because there is no present king of France.  But to deny that the present king of France is bald is to assert rather that

∃x((Gx ^ ¬Hx) ^ ∀y(Gy → x=y))

This sentence is false also.  It cannot be used to conclude that there is a present king of France who is hirsute.

Similar quick work can be done with the puzzle about existence.  “The present king of France does not exist” is equivalent to “It is not the case that the present king of France exists” and this we translate as:

¬∃x(Gx ^ ∀y(Gy → x=y))

Note that there is no need in this formula for a name that refers to nothing.  There is no name in this formula.

Finally, when George IV wished to know whether Scott was the author of Waverley, we can let “a” stand for “Scott”, and “Wx” mean “x authored Waverley”, and now assert that what the king wanted to know was whether the following is true:

∃x((Wx ^ ∀y(Wy → x=y)) ^ x=a)

In this, the part of the formula that captures the meaning of “the author of Waverley” requires no name, and so there is no issue of applying the indiscernibility of identicals rule.  (Remember that the indiscernibility of identicals rule allows the replacement of a symbolic term with an identical symbolic term.  In this formula, there is no symbolic term for “the author of Waverley”, and so even if Scott is the author of Waverley, the indiscernibility of identicals rule cannot be applied here.)

Russell has done something very clever.  He found a way to interpret a phrase like “the present king of France” as a complex logical formula; such a formula can be constructed so that it uses no names to capture the meaning of the phrase.  It is an interesting question whether Russell’s analysis should be interpreted as describing, in some sense, what is really inside our minds when we use a phrase like “The present king of France.”  That’s perhaps an issue for cognitive scientists to settle.  Our interest is that Russell inspires a new and flexible way to use first order logic to understand possible interpretations of these kinds of utterances.

Russell’s translations also suggest a surprising possibility:  perhaps many names, or even all names, are actually phrases like these that are uniquely true of one and only one thing.  That was of interest to philosophers who wanted to explain the nature of reference; it suggests that reference could be explained using the notion of a complex predicate expression being true of one thing.  That is a radical suggestion, and one that Russell developed and defended.  He proposed that the only names were the very basic primitive “this” and “that”.  All other natural language names could then be analyzed into complex phrases like those above.  This is an issue for the philosophy of language, and we will not consider it further here.

Another benefit of Russell’s translation is that it illustrates how to count with the quantifier.  This is of great interest to our logic.  Any sentence of the form “there is only one thing that is Φ” can be translated:

∃x(Φ(x)^∀y(Φ(y) → x=y))

Russell’s insight is that if only one thing is Φ, then anything that turns out to be Φ must be the same one thing.

A little ingenuity shows that we can use his insight to say, there are exactly two things that are Φ.  It might be helpful at first to separate out “there are at least two” and “there are at most two”.  These are:

∃x∃y ((Φ(x)^Φ(y)) ^ ¬x =y)

∀x∀y∀z (((Φ(x)^Φ(y))^Φ(z)) → ((x=y v x=z) v y=z))

The first sentence says, there exists a thing x and a thing y such that x has property Φ and y has property Φ and x and y are not the same thing.  This asserts there are at least two things that have property Φ.  The second sentence says for any x, y, z, if each has the property Φ, that at least one of them is the same as the other.  This asserts that there are at most two things that have property Φ.

Combine those with a conjunction, and you have the assertion at least two things are Φ, and at most two things are Φ.  That is, there are exactly two things that are Φ.

(∃x∃y ((Φ(x)^Φ(y)) ^ ¬x =y) ^ ∀x∀y∀z (((Φ(x)^Φ(y))^Φ(z)) → ((x=y v x=z) v y=z)))

That’s awkward, but it shows that we can express any particular quantity using our existing logical language.  We will be able to say, for example, that there are exactly 17 things that are Φ.  It is quite surprising to think that we do not need numbers to be able to express particular finite quantities, and that our logic is strong enough to do this.

15.6  Problems

1. For each of the following, describe whether the relation is reflexive, symmetric, or transitive.  If it lacks any of these properties, give an example of where the property would fail for the relation.  (That is, if you say a relation is not symmetric, for example, then give an example of an exception.)  Assume a domain of discourse of humans.

1. … is the sibling of …
2. … is the mother of …
3. … is the same nationality as …
4. … is older than …
5. … is in love with …

2. Make your own key and then translate the following into our logical language.  You should use a function in your translation of each sentence that has an implicit function.

1. The mother of Ludwig is musical.
2. Ludwig is not musical.
3. Ludwig’s paternal grandmother is musical, but his maternal grandmother is not.
4. Ludwig’s father is taller than his mother.
5. Ludwig’s mother is not taller than Ludwig, or his father.
6. Ludwig’s mother is not Ludwig’s father.
7. Someone is Ludwig’s mother.
8. Someone is someone’s mother.
9. Everyone has a mother.
10. No one is the mother of everyone.

3. Provide your own key and translate the following into our logic.  This will require multiple quantifiers.

1. Everyone is friends with someone.
2. Someone is friends with someone.
3. Someone is friends with everyone.
4. Everyone is friends with everyone.
5. No one is friends with everyone.

4. Use Russell’s interpretation to translate the following expressions.  Make your own key.

1. The Emperor of New York is rotund.
2. The Emperor of New Jersey is not rotund.
3. The Emperor of New York is not the Emperor of New Jersey.
4. There is no Emperor of New York but there is an Emperor of New Jersey.
5. There are two and only two Emperors of New York.

5. Use our logic to express the claim:  exactly three things have property F.

6. Consider this sentence from The Phaedo by Plato, in which Phaedo praises Socrates: “Such was the end, Echecrates, of our friend; concerning whom I may truly say, that of all the men of his time whom I have known, he was the wisest and most just.” Can you capture the comparison “he was the wisest and most just”? What is of interest here is that we have seen how to use quantifiers and identity to say something like, “other than”. This will be needed for a more accurate translation. Let the domain of discourse be, people whom Phaedo knew. You might want to translate this with a predicates to express “x is at least as wise as y” and “x is at least as just as y” before attempting the more difficult but more accurate translation with predicates “x is wiser than y” and “x is more just than y”.