CHAPTER 2: The Behavior of Gases
2.4.1 Distribution of Gas Molecules in an Enclosed Volume
2.4.2 Compressibility of Gases
Chapter 2 provides an overview of the behaviors of gases that are key to understanding the operation of vacuum systems. After you read this chapter, you will be able to:
- Identify the states of matter and describe characteristics of the underlying molecular behaviors in each state.
- Convert pressure measurements from one unit of measure to another.
- Describe the underlying assumptions related to the kinetic theory of gases.
- Explain the relationship between molecular density and pressure.
- Explain the effect of temperature on the shape of speed distribution for gas molecules.
- Apply Boyle’s law, Charles’s law, Gay-Lussac’s and the ideal gas law to solve for unknown system parameters.
- Apply Dalton’s law to relate partial pressures of gas constituents and the total pressure.
- Define the term mean free path and explain how it changes as the pressure decreases.
- Describe the processes of adsorption, desorption, diffusion and permeation.
- Describe the differences in the thermal conductivities of air, argon and helium.
- Explain the processes associated with vapor pressure and how changes in temperature impact vapor pressure.
2.1 Introduction
The key to understanding the operation of vacuum systems is the ability to visualize how gases behave. This is where our discussion of vacuum systems begins. Some of this information will be familiar to you, because living on Earth teaches us many things about the behavior of gases. For example, we have observed objects being scattered on a windy day and enjoyed the cool breeze from an electric fan on a hot day. We have seen steam rising from a lake in the early morning. Each of these situations occurs because of gas molecules in motion.
We also observe varying effects due to different gases. A helium-filled balloon, for instance, rises into the air, whereas balloons filled with room air fall to the floor. Dry ice, the common name for carbon dioxide in solid form, when placed in water sublimes readily from solid to gas to create a dramatic fog effect. We know that air is a life sustaining gas. But other gases, like carbon monoxide, are toxic.
We have used pumps to concentrate gas in a confined space, as when we pump up the tires of a bicycle or car. We have enjoyed the benefits of a reduction in gas molecules between the walls of a Thermos bottle that slows the movement of heat and keeps liquid refreshments hot or cold. We have observed the results of matter changing from the gaseous state to the liquid state (condensation), or from the solid state to the gaseous state (sublimation). These are only a few examples, and you can probably think of many more.
The goal of this chapter is to review the laws of chemistry and physics that govern the behavior of gases. The material in this chapter will help you develop a mental picture, or model, of the behavior of gases so that you will be able to visualize what is actually happening inside a vacuum system.
2.2 States of Matter
Before we begin our study of gases, let’s briefly review concepts related to the states of matter. Matter exists in one of four states: a solid, a liquid, a gas, and a plasma. Water, plain old H2O, serves as a familiar example to address the first three states.
In its lowest energy state, water exists as ice at temperatures below 0oC at standard atmospheric pressure at sea level (1 atmosphere). The water molecules are held in a rigid structure that gives ice shape, forming a solid material. When a piece of ice is placed in a container, the ice will partially fill the container but will not take the shape of the container. The surface of the ice behaves as an interface between the molecules held in solid ice form and the air that surrounds the ice. At the ice-air interface, water molecules, if they have enough energy, can cross the solid-gas boundary. The process of a water molecule escaping from the solid structure at the ice-air interface and entering into the air is called sublimation. The process in which a water molecule in the air strikes a very cold surface and becomes frost, a solid form, is called adsorption.
When the ambient temperature is increased above the freezing point, water begins to change from the solid state to the liquid state. Water exists as a liquid between the temperatures of 0oC and 100oC at standard atmospheric pressure. As a liquid, water molecules can now move, and the water can conform to the shape of the container into which it has been placed. For example, water placed in a pitcher conforms to the pitcher’s shape. The surface of water behaves as an interface between the water below and the air above. At this water-air interface, water molecules, if they have enough energy, can cross the liquid-gas boundary. If the movement of the water molecules is from the liquid state to the vapor state, then the process is called evaporation. Conversely, water molecules can move from the vapor phase to the liquid phase. We know this process as condensation.
At 100oC and standard atmospheric pressure, the boiling point of water is reached. As more energy is added, the temperature of the water will remain at the boiling point until all the water is converted to a vapor. When in the gaseous state, the water vapor (steam) can now fill the entire enclosed space above the boiling water. In the gaseous state, water molecules are able to move independently. It is the behaviors of water vapor and other gases that we will study in the chapters to follow.
In the last state of matter, plasma, the gas molecules are ionized, forming a mixture of particles. There are electrons, ions, radicals, neutrals, and other energetic particles. Plasmas hold the promise of energy generation through fusion and are used in a variety of manufacturing processes that produce products we use every day. Plasma is a fascinating state of matter and one that is the basis for important vacuum-based processes.
Looking at the periodic table of elements, illustrated in Figure 2.1, we find elements that exist naturally in one of three states of matter, that is, solid, liquid, or gas. A majority of the elements exist as solids at the normal temperature and pressure (NTP) condition, that is defined as 20oC and 1 atmosphere (101,325 Pa): copper, iron, and silicon are examples. Only two elements, mercury and bromine, exist at room temperature as a liquid. The remaining elements exist as gases at room temperature, for example nitrogen, oxygen, and argon.
2.3 Gas Pressure
A gas is made up of many gas molecules in rapid motion. Inside a closed chamber, the gas molecules collide with each other and with the chamber walls. Each collision with the chamber wall exerts a small force on the chamber wall as shown in Figure 2.2. The cumulative effect of all the molecules-wall collisions can be expressed as a force per unit area, or pressure, such as pounds-per-square-inch, or psi:
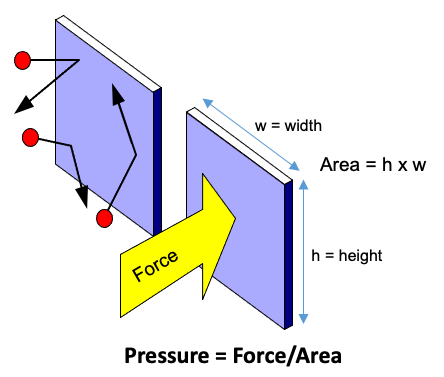
There are a great many units of measure used to specify the pressure of a gas. In the United States, the most familiar units are pounds per square inch (psi) and inches of mercury (in Hg). For example, the air pressure in car tires is specified in psi. Tire pressure is also what is called gage pressure or pressure measured in reference to the atmospheric pressure. This means that a tire pressure of 30 psi (or 30 psig), for example, is 30 psi higher than the local atmospheric pressure.
In contrast, absolute pressure is measured with reference to ideal zero pressure. Absolute pressure can be measured in units of atmospheres, torr, bar, mbar, and pascal. The pressure unit, torr, is often used in the United States and is the standard unit of pressure used in this textbook. In other parts of the world that have adopted the Systeme international des unites (SI), the standard unit of pressure is newton per square meter (N/m2) or pascal (Pa), although millibar (mbar) is used as well.
It is important for you to be able to convert from one system of units to another. The following pressures are equal to 1 atm of pressure:
1 atm = 760 Torr
= 101,325 Pa (N/m2)
= 101.325 kPa
= 1.01325 bar
= 1013.25 mbar
1 mmHg = 1.0000004 Torr (approximately 1 Torr)
Some books on vacuum technology give conversion tables for equating a pressure value in one system of units to an equivalent pressure value in another. This is helpful when you happen to have the table with you or have committed the table to memory. It is also useful to understand how to convert units of measurement. Unit conversion is based on the mathematical fact that multiplying the original pressure by the number 1 does not change the value of the original pressure. The ratio of 1 atm/760 Torr is exactly equal to 1, and the ratio of 760 Torr/1 atm also equals 1. The trick is to find the right form of the number 1. The form of 1 that should be used has 1 atm expressed in the new unit of pressure in the numerator and 1 atm expressed in the original unit of pressure in the denominator. The original pressure is then multiplied by this ratio. Mathematically, it can be expressed as follows:
The following example illustrates how using the method adapted from dimensional analysis works. Note that the original units should cancel, leaving only the new unit of pressure.
Convert 100 Torr to pascals.
Solution:
To convert pressure in torr to an equivalent pressure in pascals, we need to know, from memory or a table, the number of each unit in one atm.
The pressure unit torr (Torr) is our original pressure and the pressure unit pascal (Pa) is our new pressure unit. Hence
Despite the myriad of pressure units, one would think that measuring pressure in a chamber would be no more complicated than measuring temperature. One would reasonably expect that just like thermometers which are used for a variety of purposes and to measure different temperature ranges, pressure gauges are also available in a variety of types. However, as we will see, accurately measuring the pressure of a gas is not a trivial task, and is certainly more complex than measuring temperature.
In the rough vacuum regime (760 Torr to 1 millitorr), there are basically two types of pressure gauges: direct reading gauges and indirect reading pressure gauges.
Direct reading gauges measure the force exerted on a surface by the gas molecules. One example of a direct reading gauge is a Bourdon gauge. A Bourdon gauge is a purely mechanical gauge that uses a curved copper tube which deflects in response to the difference between atmospheric pressure on the outside and the chamber pressure on the inside. Another type of direct reading gauge is a capacitance diaphragm gauge, also known as a capacitance manometer. In a capacitance diaphragm gauge, a thin diaphragm is deformed by the force exerted by the gas molecules. This deformation changes the capacitance between the diaphragm and a reference electrode. The gauge controller electronics converts this change in capacitance into a pressure reading.
One type of indirect reading gauge uses the heat conduction property of gases to determine the density of the gas which infers the pressure in the chamber. The more gas molecules, the greater the rate of heat transfer, and thus the higher the pressure. Thermocouple and Pirani pressure gauges are examples of indirect reading pressure gauges.
In the high vacuum regime (pressures less than 1 millitorr), neither mechanical force nor the heat transfer mechanism can be used to measure pressure. To measure pressure in the high vacuum regime, gas molecules are converted from neutral atoms and molecules to ions. The ions are then collected, and the resulting electrical current is measured. The amount of current is converted to a pressure reading. A decrease in the current corresponds to a decrease in pressure.
The heat-conduction properties and the ease of ionization of gases differ based on the type of gas. Therefore, the pressure reading obtained will have to be adjusted depending on the gas or gas mixture. This makes accurate pressure measurement more complex than just reading a number on the pressure readout or display. We will talk more about this later in the book.
In the next section, we will start developing a mental picture of how gases behave. Our mental picture will be based on the kinetic theory of gases.
2.4 Kinetic Theory of Gases
The kinetic theory of gases attempts to explain the physical behavior of gases. As is typical of theories in science, it is based on a set of assumptions. In the case of the kinetic theory of gases, the underlying assumptions include the following:
- Gases are composed of a very large number of separate, independent atoms or molecules that are in constant, straight-line motion. These molecules are so widely spaced that, on the average, the total volume of the molecules is very small compared to the volume of the space those molecules are contained within.
- In the absence of collisions, the gas atoms and molecules display no attraction, or repulsion, toward one another.
- The straight-line motion of the gas molecules may be interrupted by collisions with other gas molecules or with the walls of the chamber enclosing the gas. The collisions are assumed to be completely elastic, resulting in no energy being converted to heat or another form of energy or a change in the atoms, or molecules, involved in the collision.
- Because gas molecules are in constant motion, they possess a certain amount of kinetic energy. Since the gas molecules can have different velocities, each gas molecule can have a different kinetic energy. The total kinetic energy possessed by the gas is proportional to the temperature of the gas in units of Kelvin (K) and is a function of the combined molecular velocities of all the gas atoms, or molecules, in the chamber. The underlying speeds of the gas molecules also vary by molecule type at any given temperature. Heavier molecules move on average more slowly than lighter molecules at the same temperature.
Sometimes it is helpful to draw a picture to help visualize this concept. First, draw an enclosed space of any shape that we will call the “chamber.” Inside this chamber, draw small circles to represent the gas molecules. Since the gas molecules are not static but in motion, we can represent this motion with arrows to represent the direction of travel and the speed at which it is traveling (length of the arrow) as shown in Figure 2.3. Some of the gas molecules will collide with each other, and some will collide with the walls of the chamber.
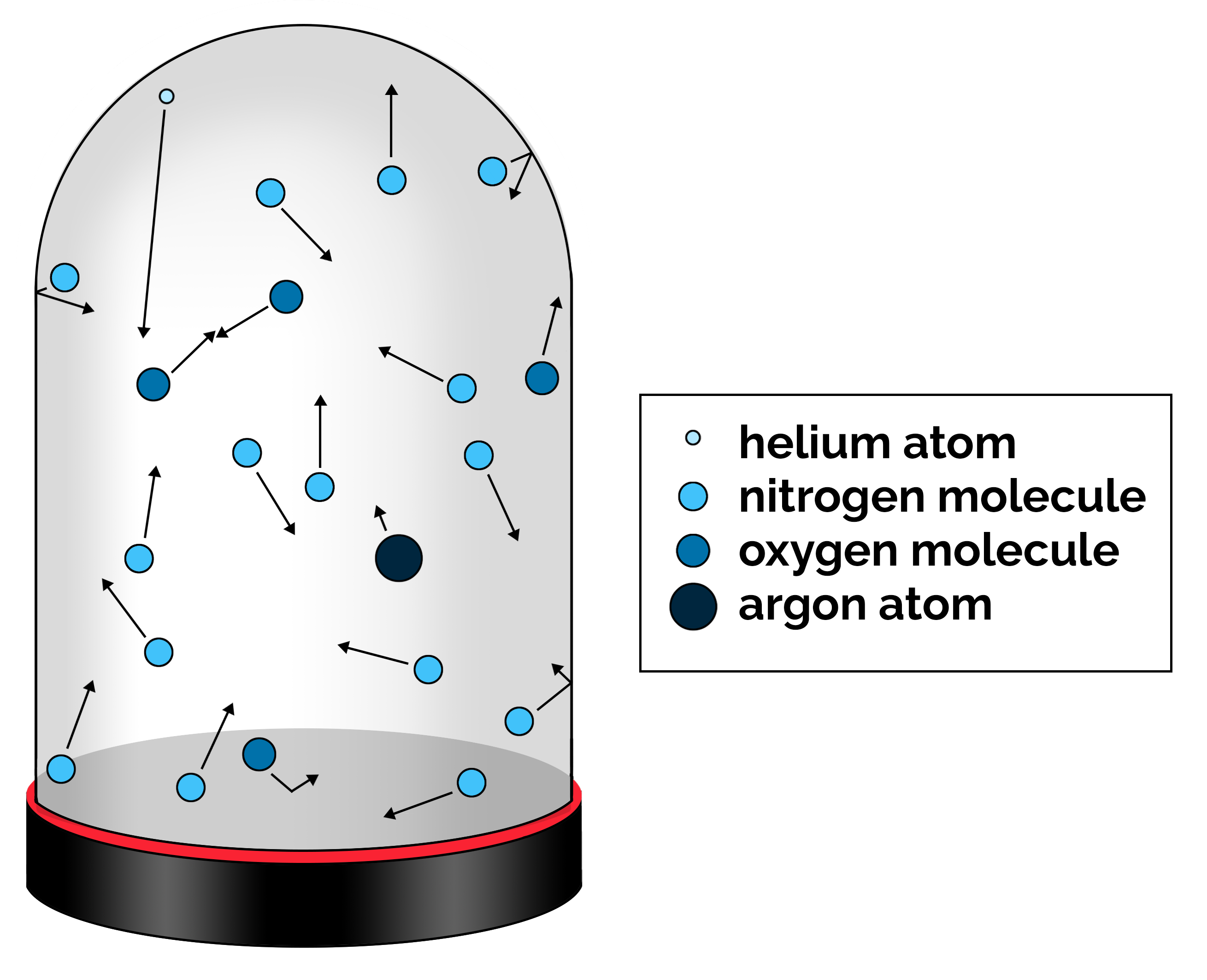
The kinetic theory of gases can be used to explain the following properties of gases:
-
- Gases fill a chamber completely, irrespective of pressure and the shape of the chamber.
- Gases are compressible (relates to Boyle’s Law).
- Gases expand/contract with changes in temperature (relates to Charles’s Law).
- Gases of equal volume and pressure have an equal number of molecules (Avogadro’s Law).
- The total pressure of a mixture of gases is equal to the sum of the partial pressures of each gas in the mixture (Dalton’s Law).
2.4.1 Distribution of Gas Molecules in an Enclosed Volume
When a certain amount of gas is placed within an enclosed volume or chamber, the gas fills the entire volume and the population density of gas molecules is uniform throughout the chamber. If this were not true, there would be areas of greater concentration of gas molecules and areas of lesser concentration. This concentration difference would produce a flux that would cause the gas molecules to move from areas of higher concentration to areas of lesser concentration. This movement of gas molecules would continue until the concentration difference and the flux are reduced to zero. Hence, the density of gas molecules must be uniform throughout the entire enclosed volume.
The density of gas molecules varies with pressure. The relationship between pressure and molecular density is shown in Table 2.1.
Table 2.1. Molecular density as a function of absolute pressure.
|
Pressure (Torr) |
# of Molecules Per Cubic Centimeter |
|---|---|
|
760 |
3 x 1019 |
|
1 |
4 x 1016 |
|
1 x 10-3 |
4 x 1013 |
|
1 x 10-6 |
4 x 1010 |
|
1 x 10-9 |
4 x 107 |
At 760 Torr, there are approximately 3 x 1019 air molecules per cubic centimeter, about 30 million trillion molecules. That is a lot of gas molecules and they are constantly in motion and are bumping into each other as well as nearby surfaces. In fact, they are so close together that, on average, each molecule travels only 6 x 10-5 millimeters before colliding with another molecule. When a chamber is sealed with air at atmospheric pressure, the molecular collisions occurring within the chamber volume are overwhelmingly gas molecules running into each other compared to gas molecules striking the interior walls of the chamber.
If we reduce the pressure by six orders of magnitude to a pressure of one millitorr, the number of gas molecules per cubic centimeter is approximately 4 x 1013, or 40 trillion. That still seems like a lot of gas molecules, but at this pressure, the distance traveled by gas molecules between collisions approaches 2 inches, or approximately 5 centimeters. In large chambers, the number of gas molecules to gas molecule collisions dominates, whereas there are proportionately fewer collisions against chamber walls.
If the pressure is further reduced to 1 x 10-9 Torr, another reduction of six orders of magnitude, the number of gas molecules per cubic centimeter is now 4 x 107, or 40 million. That is still a lot of gas molecules in a small space, but now the distance that gas molecules travel between collisions with each other is 31 miles (50 kilometers), a distance much greater than the dimensions of almost any chamber. At these pressures, the collisions between gas molecules and the chamber walls dominate. This change from majority of gas molecule to gas molecule collisions at atmospheric pressure to majority of gas molecule to chamber wall collisions at very low pressures is important in processes carried out at these very low pressures.
2.4.2 Compressibility of Gases
One of the qualities that distinguishes gases from solids and liquids is compressibility. From our life experiences, we know this to be true. For example, we have probably experienced the compressing of air when pumping up a bicycle or car tire.
The compressibility of gases can be explained quite easily using the kinetic theory of gases. Gas molecules are seen as very small molecules separated by great distances compared to their size. Reducing the volume enclosing the gas molecules crowds them together. As the gas molecules move within a smaller volume, the number of collisions between them increases, as does the number of collisions between the gas molecules and the chamber walls. The cumulative effect of all the collisions between the gas molecules and the wall of the chamber creates a greater force on the chamber wall, or chamber pressure, as shown in Figure 2.4.
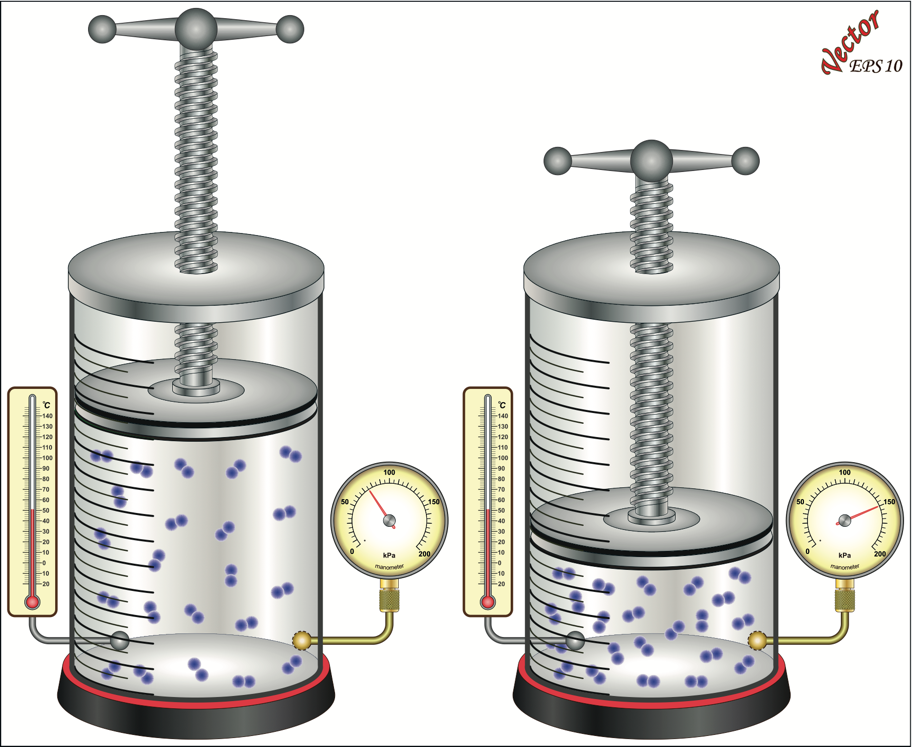
The relationship between the volume of gas and the absolute pressure exerted by a constant amount of gas is stated in Boyle’s Law. Boyle's law states that if the temperature and the amount of gas are held constant, the volume of gas is inversely proportional to the pressure exerted by the gas. The relationship can be expressed in equation form as
The proportionality can be changed to an equality by inserting a proportionality constant, k. Hence,
If a fixed volume of gas at a constant temperature is compressed or expanded, then
where Pi and Vi is the initial or first condition, and
where Pf and Vf is the final or second condition.
Since the two equations equal the same constant, we can set an equals sign between them. This yields,
This is the mathematical statement of Boyle’s law.
If the amount of gas and the temperature are constant, we can use Boyle’s law to solve for the missing parameter if the other three parameters are known. For example, if we know the initial absolute pressure and volume and the final volume, we can solve Equation 2.3 for Pf. This yields,
It is important to note that Pi and Pf represent absolute pressure in equation 2.4.
Before doing numerical examples, let's first see how an ideal gas behaves when the temperature is held constant and the volume of the gas changes. We are going to use the embedded "Introduction to Gases" Simulation 2.1 below. When you open the simulation, choose the "Laws" option at the bottom of the simulation. Introduce a small number of gas molecules into the chamber by using the simulated pump. One "pump" of gas is enough. Choose the option to hold temperature constant and increase the volume to the maximum value allowed. Note the pressure indicated on the pressure gauge. Then reduce the volume to half of the original volume and note how the pressure in the chamber changes. You should be able to see that cutting the volume in half results in doubling the pressure if temperature is held constant. This is consistent with Equation 2.4.
Simulation 2.1. Introduction to Gases Simulation. PhET Interactive Simulations, University of Colorado Boulder, https://phet.colorado.edu.
It is important to note that a gage pressure value must be converted to an absolute pressure value when performing a calculation using Boyle's law.
A gas is compressed at a constant temperature from an initial volume of 1.5 liters to 1.0 liter. If the initial pressure is 800 Torr, what is the final pressure in torr?
Solution:
Using Equation 2.4,
How does Boyle’s law help explain why a bag of potato chips seems to have more air in it while in flight than on the ground at the boarding gate.
Solution:
Consider the situation of purchasing a bag of potato chips at the airport in Miami, a location that is very near sea level. The pressure within the bag when it is completely sealed and you are standing at the boarding gate should be near 1 atm. The temperature within the bag can be assumed to be the same as the temperature inside the terminal which may be close to 20°C.
After the plane takes off and reaches cruising altitude, the cabin is pressurized to approximately 0.7 to 0.8 atm in order to maintain a suitable level of oxygen for passengers. The temperature in the plane’s cabin will likely be close to 20°C.
A potato chip bag is a relatively flexible material. Since the temperature in the terminal and the temperature in the plane’s cabin is the same, we can use Boyle’s law to understand what should happen to the sealed bag.
Pi = 1 atm within the sealed potato chip bag when you’re at the boarding gate in the terminal
Pf = 0.8 atm within the sealed potato chip bag when the plane is at cruising altitude
Vi = volume of the sealed potato chip bag at the boarding gate
Vf = volume of the sealed potato chip bag at cruising altitude
Boyle’s law predicts that the volume of the bag will be 1.25 times larger when the plane is at cruising altitude than its volume when you were standing at the boarding gate. An important point here is that even though the volume of the sealed bag is expanded and looks like it contains more air during an airplane flight, it still contains practically the same number of gas molecules as it did when you were standing at the boarding gate!
2.4.3 Effects of Temperature
Since gas molecules are in constant motion, each gas molecule has a certain amount of kinetic energy. The kinetic energy of a gas molecule is equal to
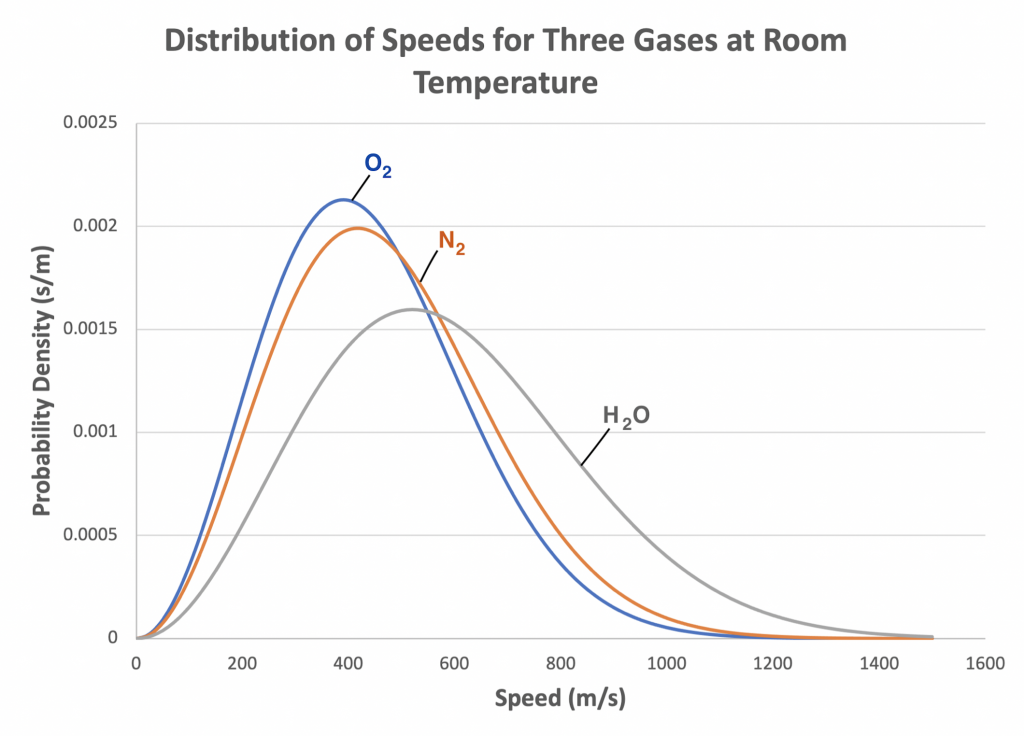
where m is the mass of the gas molecule and v is the velocity magnitude or speed of the gas molecule. The gas molecules in the chamber do not all have the same velocity or speed. The distribution of the velocities of gas molecules follows a curve known as the Maxwell-Boltzmann distribution. Different gas types will have slightly different Maxwell-Boltzmann distributions.
Figure 2.5 shows the velocity distribution for four gases at the same temperature. Examining the graph, we see that the number of gas molecules with zero speed is essentially zero because few, if any, gas molecules are standing still at any instant. Moving to the right along the horizontal axis represents the increasing speeds of individual gas molecules at a given temperature. The vertical axis represents the probability that a molecule has a particular speed. In other words, for a given speed, out of all the gas molecules present, a certain number of them, not all of them, are moving at that speed. The graph peaks at a point that represents the most probable speed - that is the speed at which the largest number of molecules out of all the gas molecules present are moving. Moving right from the most probably speed, the numbers of molecules present that are moving at higher speeds decreases and approaches zero. The average speed of the gas molecules is higher than the most probably speed because the curve is not symmetric.
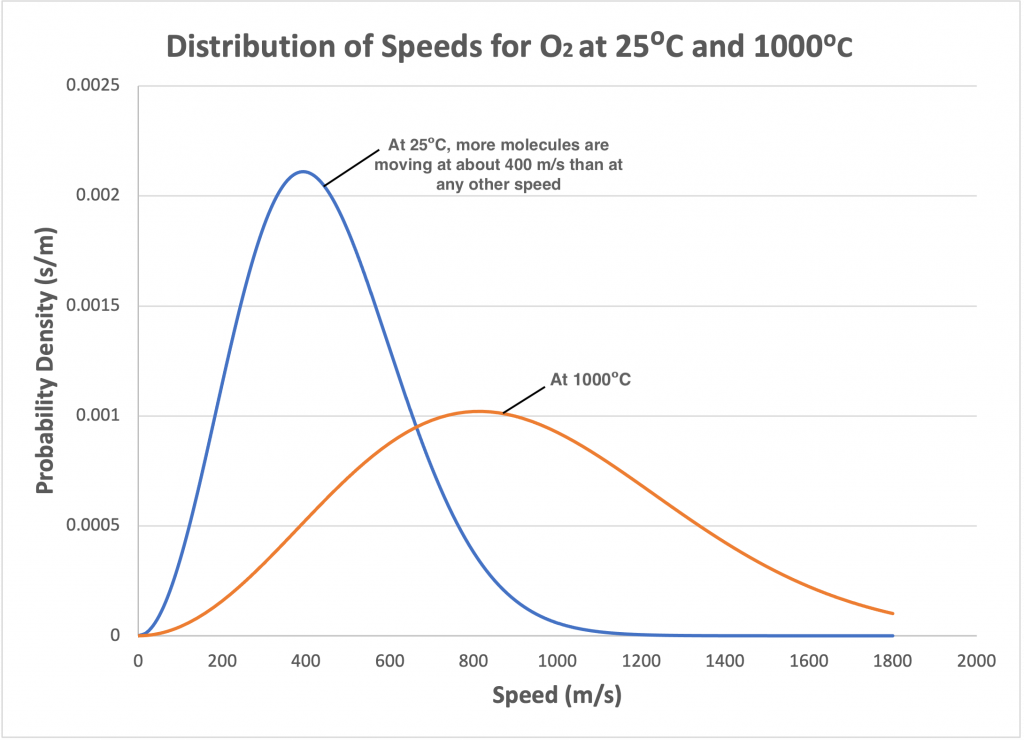
When the temperature of a gas changes, the shape of the curve described by the Maxwell-Boltzmann distribution changes. For example, if the temperature of a gas is increased, the kinetic energy of the gas molecules increases corresponding to increased molecule speeds. The shape of the curve flattens out, and more gas molecules exhibit higher speeds. Corresponding increases are seen in both the most probable speed and the average speed. Figure 2.6 shows the effect of increasing or decreasing temperatures on the speed distribution for a gas.
The "Gas Properties" Simulation 2.2 below also shows the effects of temperature change on the speed distribution of molecules in a gas. To run the simulation, open the "Energy" tab and introduce gas into the system by using the bicycle pump. Note the current temperature, average speed and real-time speed distribution graph. Now, increase the temperature by heating the bucket and observe what happens to the temperature, average speed and the shape of the speed distribution. As temperature increases, you should be able to see that the average speed increases and the distribution of the speeds becomes wider, as a larger number of molecules have higher speeds.
Simulation 2.2. Gas Properties Simulation. PhET Interactive Simulations, University of Colorado Boulder, https://phet.colorado.edu.
The relationship between volume and temperature, at a constant pressure is given by Charles’s law, which is named after the eighteenth-century French chemist Jacques Alexander Charles. Charles’s law states that the volume of a gas is directly proportional to the absolute temperature at a constant pressure. Mathematically, Charles’s law can be expressed as
where V is the volume of the gas and T is the absolute temperature. Charles’s law can also be expressed as an equality:
If gas is kept at a constant pressure while its volume and temperature change, then
where Vi and Ti is the initial or first condition, and
where Vf and Tf is the final or second condition.
Since the two equations equal the same constant, we can set the equal sign between them. This yields,
This is the mathematical statement of Charles's law.
If the amount of gas and the pressure are constant, we can use Charles's law to solve for the missing parameter if the other three parameters are known. For example, if we know the initial volume and temperature and the final temperature, we can solve Equation 2.8 for final volume Vf. This yields,
It is important to note that when using the equation for Charles’s law, temperatures must be in units of Kelvin. That is, temperature given in Celsius or Fahrenheit must be first converted to Kelvin in order to perform the calculation using Charles's law.
A certain amount of gas occupies a volume of 3.0 liters at a temperature of 30°C and a pressure of 1 atm (atmosphere). How many liters will it occupy at a temperature of 75°C and an absolute pressure of 1 atm? Assume the pressure remains constant.
Solution:
From the data given, the pressure remains constant, while volume and temperature change. According to Charles’s law given by Equation 2.8,
Solving for Vf,
Before this calculation can be performed, all temperatures must be converted from degrees Celsius to Kelvin:
Then,
Use Charles’s law to explain why an empty plastic water bottle collapses when it remains in a space that cools off.
Solution:
Consider a situation in which you are traveling in a car and drinking water from a plastic bottle. When you are finished drinking the water, you screw the cap on the bottle. The temperature inside the car is 20°C. The atmospheric pressure experienced inside the car is nearly identical to the pressure outside the car.
You happen to be traveling in Minnesota during January, and it is very cold outside. The car is parked, turned off and left to sit outside overnight. The capped bottle is left in the car while the temperature inside the car drops to -25°C.
A plastic water bottle can be a relatively flexible material. Since the atmospheric pressure experienced inside and outside the car is nearly identical, we can use Charles’s law to understand what should happen to the water bottle as the temperature in the car cools.
Ti = 20°C within the capped water bottle when the car is turned off
Ti = 20°C = 20 +273K = 293K
Tf = -25°C within the capped water bottle after the car sits outside overnight
Tf = -25°C = -25 +273K = 248K
Vi = volume of the capped water bottle when the car is turned off
Vf = volume of the capped water bottle after the car sits outside overnight
Charles’s law predicts that the volume of the water bottle will be 15 percent smaller after sitting in the cold car overnight. An important point here is that even though the bottle’s volume shrinks and looks like it contains less air, it contains roughly the same amount of molecules as it did before the car started cooling.
And finally, Gay-Lussac’s law , also known as Amonton's law, describes how the absolute pressure of a gas depends on its temperature while the volume of the gas is held constant. According to this law, the absolute pressure of a gas at a constant volume is directly proportional to the absolute temperature. Stated in equation form,
or using a proportionality constant,
If gas is kept at constant volume, while its pressure and temperature change, then
where Pi and Ti is the initial or first condition, and
where Pf and Tf is the final or second condition.
Since the two equations equal the same constant, we can set an equals sign between them. This yields,
This is the mathematical statement of Gay-Lussac’s law.
If the amount of gas and the volume are constant, we can use Gay-Lussac’s law to solve for the missing parameter if the other three parameters are known. For example, if we know the initial absolute pressure and temperature and the final temperature, we can solve Equation 2.12 for final absolute pressure Pf. This yields,
This can be illustrated by using the "Introduction to Gases" Simulation 2.3 below. When you open the simulation, choose the "Laws" option at the bottom of the simulation. Introduce a small number of gas molecules into the chamber by using the simulated pump. One "pump" of gas is enough. Choose the option to hold volume constant. Take a note of the current pressure and temperature values. Use the bucket control below the chamber to increase the temperature. You should be able to see that as temperature increases, pressure is also rising.
Simulation 2.3. Introduction to Gases Simulation. PhET Interactive Simulations, University of Colorado Boulder, https://phet.colorado.edu.
A gas exerts a pressure of 500 Torr at 25°C. What pressure in torr will the gas exert if the temperature is raised to 40°C? Assume the volume remains constant.
Solution:
From Gay-Lussac’s law given, as by Equation 2.12,
Solving for Pf,
The temperatures, given in Celsius, must be converted to absolute temperatures in degrees Kelvin.
Substituting for Pi, Ti, and Tf in the Pf equation,
Use Gay Lussac’s law to calculate the pressure inside of a glass bottle that sat in a cold car overnight. Assume the cap is secured to the bottle just before the bottle is transferred to a warmer environment.
Solution:
Since glass is a much more rigid material than plastics, a glass bottle capped off will behave like a constant volume. Assume that the glass bottle that sits in the cold car overnight gets to a temperature of -25°C. Let’s assume that the atmospheric pressure is 740 Torr, which is the nominal atmospheric pressure experienced in much of Minnesota. 740 Torr can be assumed to be the pressure inside the cold glass bottle when you secure the cap on the bottle. You bring the bottle into a building where the temperature is 20°C and allow the bottle and the air inside of it to warm up.
Use Gay-Lussac’s law to calculate the pressure inside of the glass bottle when the air inside of it warms up to 20°C.
Gay-Lussac’s law predicts that the pressure inside the capped glass water bottle will increase after it is transferred from a cold environment to a warm environment. Unlike the previous two examples, there won’t be a visual cue of the bottle changing shape that let’s you know that the pressure increased inside the bottle. You may be able to release the cap in a manner that allows you to visualize that a change has occurred, for example, into a balloon. As with the previous two examples, even though the air within the bottle is under a higher pressure after the air inside the bottle warms up, the bottle still contains roughly the same amount of molecules as it did at the point the cold bottle was capped.
2.4.4 Gases of Equal Volume and Pressure
Amedeo Avogadro proposed Avogadro’s law, which states that equal volumes of gases at the same temperature and pressure contain equal numbers of gas molecules. Avogadro’s law was subsequently used to show that gases such as hydrogen, oxygen, and chlorine must be diatomic in structure.
If we examine one mole, that is, an amount of 6.02x1023 atoms or molecules, of a gas at a temperature of 0°C, or 273 K, and a pressure of one standard atmosphere, or 760 Torr, we can measure the molar volume at conditions defined as Standard Temperature and Pressure (STP). Table 2.2 gives the molar volume for some common gases. From the results of these measurements plus measurements for other gases, the average volume occupied by one mole of gas at STP is 22.4 liters, and this value is therefore taken to be the molar volume of an ideal gas at STP.
Table 2.2. Molar volumes for some common gases.
|
Gas, symbol |
Molar Volume in liters |
|---|---|
|
Argon, Ar |
22.397 |
|
Carbon Dioxide, CO2 |
22.260 |
|
Helium, He |
22.434 |
|
Hydrogen, H2 |
22.433 |
|
Nitrogen, N2 |
22.402 |
|
Oxygen, O2 |
22.397 |
(Source: Adapted from Brady, General Chemistry, Table 11.1, p. 343.)
2.4.5 Mixture of Gases
When two or more gases that do not react chemically are placed in the same confined space, the pressure exerted by each gas in the mixture is the same as it would be if it were the only gas in the confined space. The pressure exerted by each gas in a mixture is called its partial pressure. The total pressure is equal to the sum of the partial pressures of each gas in the mixture. This statement is called Dalton’s law of partial pressure. Mathematically, it can be expressed as,
where
P total = the total pressure of the gas mixture,
P gas A = the partial pressure of gas A,
P gas B = the partial pressure of gas B,
and so on.
Consider the composition of our atmosphere at STP. Table 2.3 lists the gases that make up our atmosphere, the percentage by volume, and the partial pressure of each constituent gas. If we add all the partial pressures for the constituent gases that make up air, the sum of the partial pressures is approximately 760 Torr.
Table 2.3. Gas composition of air at STP.
|
Gas |
Symbol |
Percent by Volume |
Partial Pressure (Torr) |
|---|---|---|---|
|
Nitrogen |
N2 |
78 |
593 |
|
Oxygen |
O2 |
21 |
158 |
|
Argon |
Ar |
0.94 |
7.1 |
|
Carbon Dioxide |
CO2 |
0.03 |
0.25 |
|
Helium |
He |
0.0005 |
4 x 10-3 |
|
Hydrogen |
H2 |
0.00005 |
4 x 10-4 |
|
Water |
H2O |
0 - 2.3 |
0 - 17.5 |
Predict the partial pressures of the gases making up the atmosphere in the cabin of an airplane at cruising altitude. Assume that the percent by volume occupied by the gases is unchanged in the airplane’s cabin. Ignore the partial pressure of water.
Solution:
A plane’s cabin pressure at cruising altitude is approximately 0.8 atm.
We could show the partial pressures of each of the gases in units of atmospheres. In order to compare the results to the ones listed in Table 2.4, we will convert units of atmospheres to units of torr.
Convert the plane’s cabin pressure at cruising altitude from atmospheres to torr.
- 1 atm = 760 Torr
- 1 atm / 760 Torr = 760 Torr / 1 atm = 1
Any value multiplied by 1 is itself.
- 0.8 atm x 1 = 0.8 atm * (760 Torr / 1 atm) = 608 Torr
The plane’s cabin pressure at cruising altitude is 608 Torr. Multiply the percent volume of each gas in the composition of air by the cabin pressure at cruising altitude.
Table 2.4. Gas Composition of air in plane at cruising altitude.
|
Gas |
Symbol |
Percent by Volume |
Partial Pressure (Torr) |
|---|---|---|---|
|
Nitrogen |
N2 |
78 |
474.2 |
|
Oxygen |
O2 |
21 |
127.7 |
|
Argon |
Ar |
0.94 |
5.7 |
|
Carbon Dioxide |
CO2 |
0.03 |
0.2 |
|
Helium |
He |
0.0005 |
3 x 10-3 |
|
Hydrogen |
H2 |
0.00005 |
3 x 10-4 |
The sum of these partial pressures adds up to the total pressure in the cabin at cruising altitude:
2.5 Ideal Gas Law
The three gas laws explained in Section 2.3 can be combined into one law known as the combined gas law. The combined gas law can be expressed as
As with Boyle’s law, Charles’s law, and Gay-Lussac’s law, the amount of gas is assumed to be constant. The combined gas law allows us to analyze situations where two of the three parameters change at the same time. Equation 2.15 below represents the combined gas law:
where Pi and Pf are initial and final absolute pressure, and Ti and Tf are initial and final temperature in Kelvin (K). The following example illustrates the use of the combined gas law.
A sample of gas, stored in a 0.5-liter container at 25°C, exerts a pressure of 750 Torr. What would be the pressure of the gas if the gas sample were transferred to a 1-liter container at 50°C?
Solution
Let us begin by organizing the given information in tabular form as shown below.
|
|
Initial Conditions |
Final Conditions |
|---|---|---|
|
Pressure, P |
750 Torr |
? |
|
Volume, V |
0.5 liter |
1.0 liter |
|
Temperature, T |
25 + 273 K |
50 + 273 K |
Solving the combined gas law equation (Equation 2.15) for the final pressure, Pf, yields
If we allow the amount of gas to vary, then the constant (PV/T) in the combined gas law will also vary. For example, if the number of moles of gas is doubled, the value of the constant will double. If the number of moles of gas is reduced by one half, the value of the constant in the combined gas law will likewise be reduced by one half.
If n represents the number of moles of gas, then the combined gas law can be written as
Many chemistry textbooks use the letter R to represent this other constant and they name it the universal gas constant. Hence, this relationship can be written as
Equation 2.16 is also known as the ideal gas law. Using the ideal gas law, if three of the variables are known, the fourth can be found.
The value of the universal gas constant, R, can be found experimentally by finding the volume of one mole of gas under a known condition. As was stated in Section 2.4.4, one condition that can be used is STP. Although the volume that one mole of gas occupies at STP varies somewhat for different gases, the average molar volume is 22.4 liters.
From the ideal gas law,
The universal gas constant can be expressed using other units, for example, milliliters, torr, moles, and K. This conversion can be performed as follows,
What volume will 24.0 g of nitrogen (N2) occupy at 20°C and a pressure of 0.755 atm?
Solution:
Algebraically solving the ideal gas law for volume, V, yields
Since pressure is given in atmospheres, we can use the gas law constant 0.0821 (liter∙atm)/(mol∙K) and convert the given data to the units used in this constant. Hence,
Substituting these values into the equation for volume yields,
2.6 Mean Free Path
In a process chamber at atmospheric pressure, the gas molecules are constantly colliding with one another and with the walls of the chamber. The distance traveled by a given gas molecule before colliding with another gas molecule is called the free path. The distance a gas molecule travels and the direction of travel are randomly distributed. Hence, the mean free path is the average of the free paths traveled by the gas molecules in the chamber. According to kinetic theory, this can be represented mathematically as
where λ is the mean of the free paths, d0 is the molecular diameter in meters, and n is the gas density in molecules per cubic meter.
Use the equation for λ to estimate the mean free path of air molecules at 760 Torr and 0°C.
Solution:
From a table of physical properties of gases, the molecular diameter of air molecules is 0.372 nm at T = 0°C. The density of air at 760 Torr is approximately 3 x 1025 molecules per cubic meter. Hence,
The mean free path of gas molecules is related to gas density and thus to the pressure of the gas within the chamber. The lower the pressure, the lower the density and the greater the spacing between gas molecules. In this case, because the gas molecules are more widely spaced, a gas molecule will travel a greater distance before colliding with another gas molecule. Conversely, a higher pressure means a greater density of gas molecules and a shorter distance between collisions, that is, a shorter mean free path.
If the temperature is relatively constant at 20°C, a rule-of-thumb relationship between mean free path and air pressure can be described mathematically as
where λ is in centimeters and P is in torr.
Use equation 2.18 to find the approximate mean free path of air at 760 Torr.
Solution:
Substituting 760 Torr into Equation 2.18 yields,
Note that the result obtained using Equation 2.18 is close, but not exactly equal, to the value obtained earlier using Equation 2.17. That is OK. The important idea here is the relationship between mean free path and pressure. The mean free path and the pressure are inversely related. As the pressure goes down, the mean free path goes up, and conversely, as pressure goes up, the mean free path goes down.
Why is the mean free path of atoms and molecules an important parameter in manufacturing processes? As we described in the metal evaporation process in Chapter 1, in order to create a thin film of pure metal material on a substrate surface, the metal vapor must travel from the crucible to the substrate surface without being impeded or reacting with another element along the way. Lower pressure conditions correspond to a longer mean free path as shown in Table 2.5. So lower pressure conditions enable molecules to travel longer distances without colliding with other molecules.
Table 2.5. Relationship between pressure and mean free path.
|
Pressure |
Mean Free Path |
|---|---|
|
760 Torr |
6.6 x 10-6 cm |
|
1 Torr |
5 x 10-3 cm |
|
1 x 10-1 Torr |
5 x 10-2 cm |
|
1 x 10-3 Torr |
5 cm |
|
1 x 10-6 Torr |
50 m |
|
1 x 10-9 Torr |
50 km |
2.7 Adsorption and Desorption
Adsorption and desorption are processes that occur at surfaces. Adsorption is a process whereby gas phase atoms and molecules stick to the surface of something else. The "surface" is all of the interior surface of the process chamber including the surface of the wafer, or other substrate material, being processed in the chamber. In a vacuum system, the molecules that stick to a surface are usually water vapor, because water vapor, in the form of humidity, is always found in air.
Since gas molecules are in constant motion, water molecules in the gas phase strike the surfaces in the chamber at a steady frequency. When the water molecules hit the surface, some of them will attach to the surface and are said to be adsorbed on the surface. The attachment occurs because there are stable positions for the water molecule to form a bond on the surface. In addition, the impinging atoms or molecules must give up enough of their kinetic energy to adsorb on the surface. Sometimes, the impinging atoms or molecules do not lose the required amount of kinetic energy and are quickly reflected from the surface. The likelihood that a molecule will stick to a surface varies with the gas and the surface material.
The polar nature of water molecules does not simply cause them to adhere to the chamber surfaces; they also adhere to each other in ever-weakening bonds as the layers of adsorbed molecules become thicker and thicker and more disordered. Over time, the adsorbed water molecules can form many monolayers of water molecules on surfaces. Figure 2.7 and Animation 2.1 show the hydrogen bonding between water molecules.
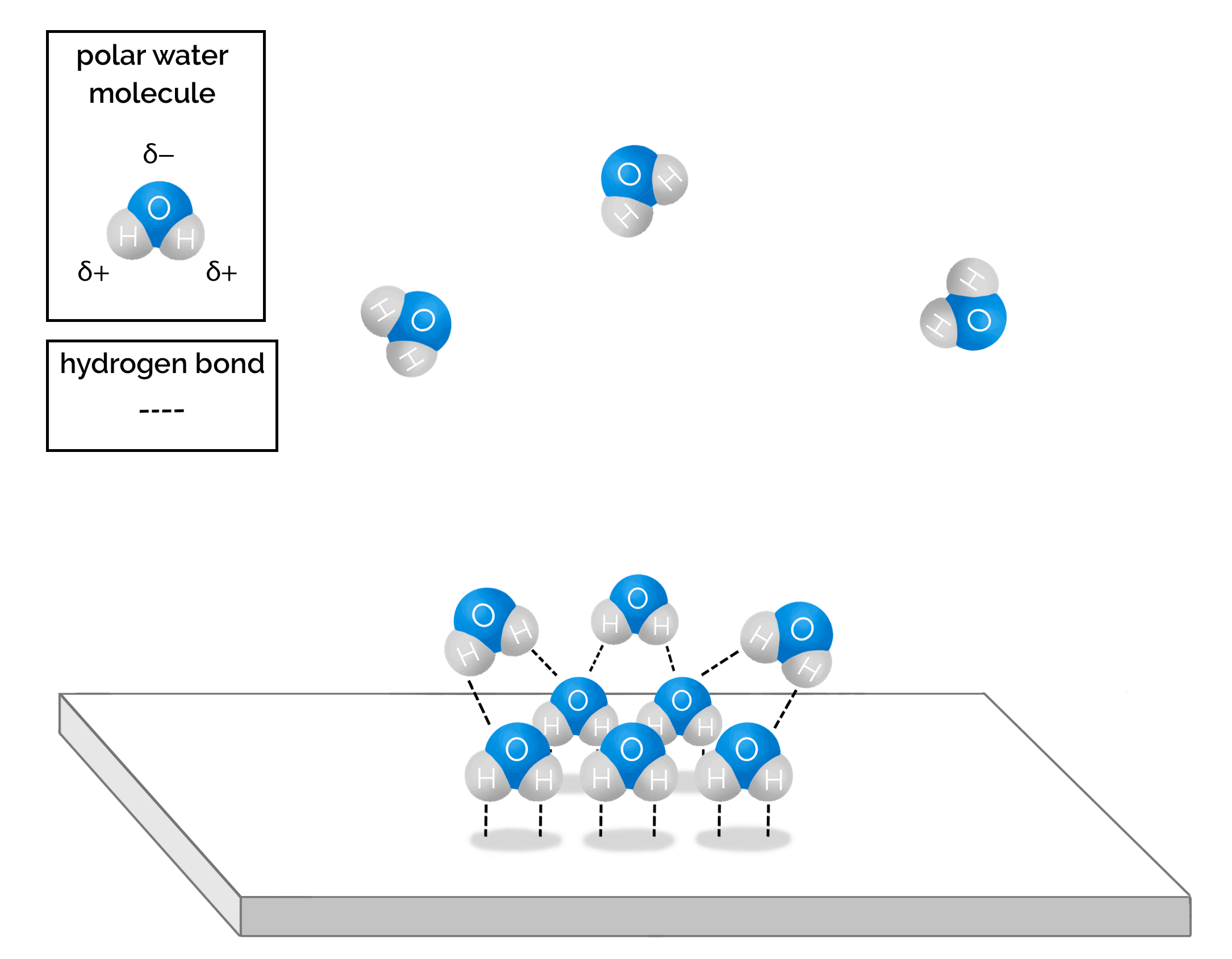
Graphics provided by Gigi Bocek, Normandale Community College.
Any material exposed to air for any length of time will come to equilibrium with the surrounding water vapor – that is, a point where the number of water molecules attaching to the surface will equal the number of water molecules leaving the surface. At this point, the surface is said to be saturated.
As a pump-down cycle proceeds to reduce pressure in the chamber, the adsorbed water molecules begin to desorb, that is, leave the surface to which they have bonded. In fact, water vapor becomes the dominant gas source and determines the gas load for the vacuum system. The weakly held outer layers will desorb quickly, and the more tightly held layers will take longer to desorb, as shown in Animation 2.2.
Desorption of water from a surface can be sped up by adding energy to the surface and the water molecules. One method is to heat the vacuum-exposed surfaces with a radiant energy source such as a heat lamp. Energy from the heat source provides the energy needed for water molecules to break the hydrogen bonds that hold them to each other. Another method is to put vacuum components into an oven or wrap their surfaces on the outside of the vacuum chamber in heating tape to thermally drive the water molecules from the vacuum-exposed surfaces. This method is called bake out.
Purging the chamber with a dry gas will also remove water adhering to the interior surface of the chamber. A gas often used for this purpose is dry nitrogen. The nitrogen gas molecules strike the surface and dislodge water molecules.
2.8 Diffusion and Permeation
Diffusion and permeation are often confused. Let’s review these phenomena and differentiate between these two terms. Both, diffusion, and permeation are shown in Animation 2.3 below.
Animation 2.3. Diffusion and Permeation Animations
 |
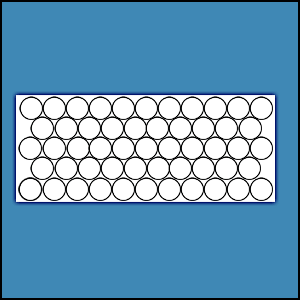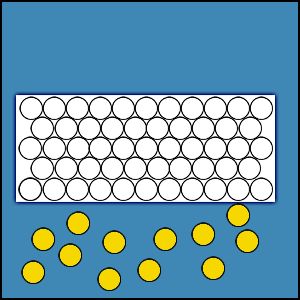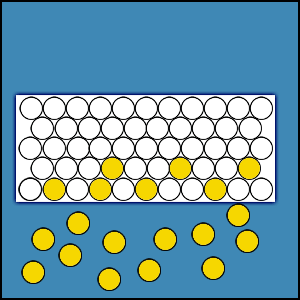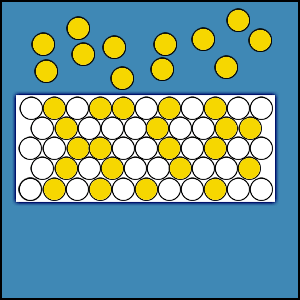 |
Diffusion is the movement of molecules within a material, whether it be a solid, liquid, or gas. Diffusion is the process by which atoms or molecules move from an area of high concentration to an area of low concentration within the material. We are familiar with some every day examples of diffusion. Perfume diffuses in the air in the room. A drop of ink diffuses when dropped into a beaker of water.
Permeation, on the other hand, is a three-step process whereby a gas molecule passes through a material, typically a solid. First, a gas molecule adsorbs onto an outer surface. Then, it is taken in, that is, absorbed, by the bulk material. Next, the molecule diffuses through the bulk material. Finally, this gas molecule desorbs from a location on the inner surface and enters the gas load. In a vacuum system, steady-state permeation acts like a constant leak.
2.9 Thermal Conductivity
The ability of a gas to conduct heat is not the same for all gases. Using the data found in Appendix B.2 of A User’s Guide to Vacuum Technology, 3rd Ed. by John F. O’Hanlon, the thermal conductivity of air which is made up of primarily nitrogen and oxygen is 24.0 mJ/(s K), while argon has a thermal conductivity of 16.6 mJ/(s K). This says that air is a much better conductor of heat than argon. On the other hand, the thermal conductivity of helium is 142.0 mJ/(s K), a value about six times greater than the thermal conductivity of air.
The thermal conductivity of gases and their ability to transfer heat varies predictably from approximately 1 Torr down to 0.001 Torr (1 milliTorr or 1mTorr). As the pressure falls below 0.001 Torr, radiation becomes the dominant mode of heat transfer. We will return to this gas parameter when we discuss pressure gauges that rely on the thermal conductivity of gases for their operation.
2.10 Vapor Pressure
When a liquid is placed in a closed container or chamber, molecules in the liquid that possess high kinetic energies (see section 2.3.3, Maxwell-Boltzmann distribution) and are located right at the surface may escape the liquid surface and accumulate as part of the total gas load in the chamber volume. Once these molecules transition from the liquid phase into a gas phase, commonly referred to as vapor phase, they exert a pressure, just like other gas molecules in the chamber. The pressure will rise initially and then gradually become constant, having reached an equilibrium vapor pressure.
This behavior of vapor pressure can be visualized in the following manner. Upon introduction of a liquid into the chamber, molecules at the surface with high kinetic energies begin to evaporate, moving from the liquid phase to the vapor phase. Once in the vapor phase, the evaporated molecules begin to exert a pressure against the walls of the chamber. As time passes, more and more molecules escape from the liquid phase to the vapor phase. At the same time, some of these molecules collide with the liquid surface where they transfer some of their energy back to the molecules in the liquid. Lacking enough energy to return to the vapor phase, these molecules once again transition back into the liquid phase. This is the process of condensation. Hence, there are two opposing processes working at the same time, evaporation of molecules from the surface to the vapor phase and condensation of molecules back to the liquid phase. When the two opposing processes are equal, the equilibrium vapor pressure has been reached, as depicted in Figure 2.8.
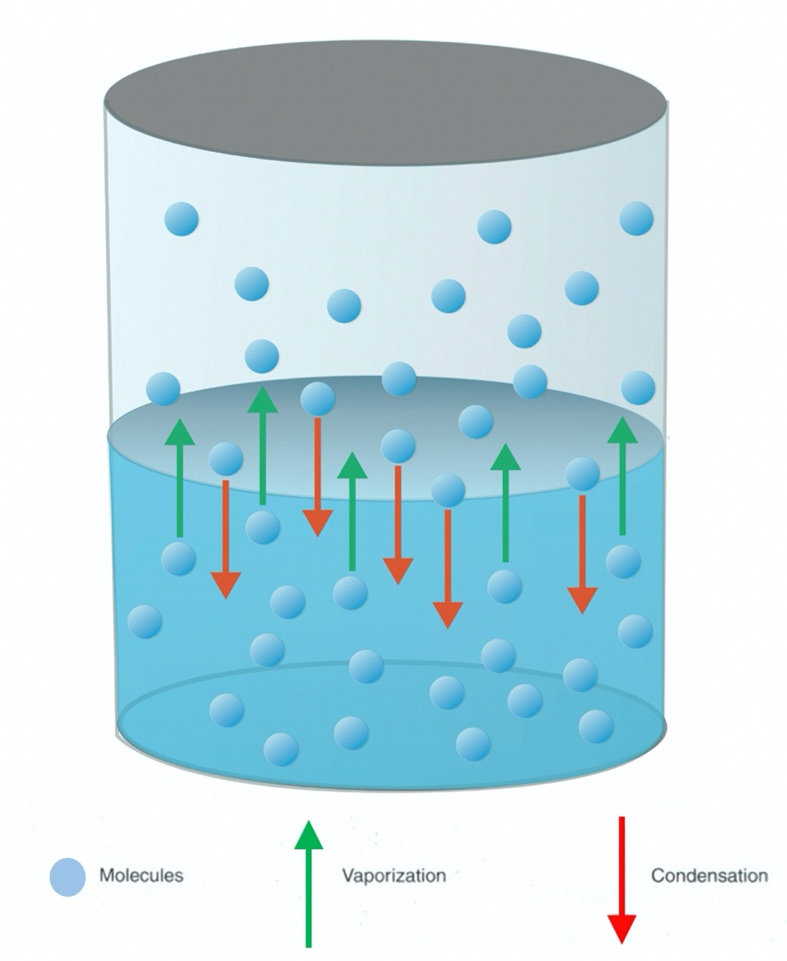
Vapor pressure is a function of temperature. The relationship between vapor pressure and temperature can be described by the following mathematical equation:
where
If temperature were to increase, then the negative term in the equation becomes smaller and the right-hand side of the equation becomes a larger number. Hence, the logarithm of the vapor pressure becomes larger, and the vapor pressure becomes greater as can be seen in Figure 2.9. On the other hand, if the temperature decreases, the negative term increases, and when subtracted from A makes the value of the right side of equation smaller. If the logarithm of the vapor pressure is smaller, then the vapor pressure must decrease.
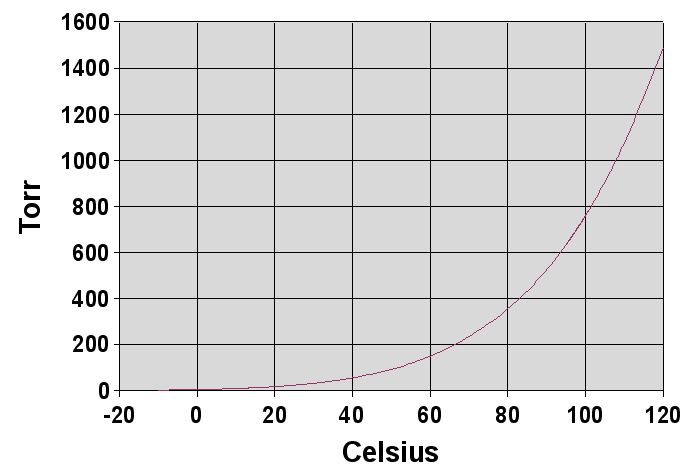
What happens when the vapor pressure of the liquid equals the pressure of the gas volume above the liquid? We have all observed what happens in cooking food. When water in a pan is heated to a high-enough temperature, it boils. Raising the temperature of the water increases the vapor pressure of the water. The boiling point is therefore the temperature at which the vapor pressure of the water equals the atmospheric pressure. At 760 Torr, water boils at 100oC, and this temperature is referred to as the normal boiling point of water. At higher than atmospheric pressures, the boiling point of water will be higher than 100oC, and conversely, at lower than atmospheric pressures, the boiling point will be lower than 100oC as shown in Figure 2.10.
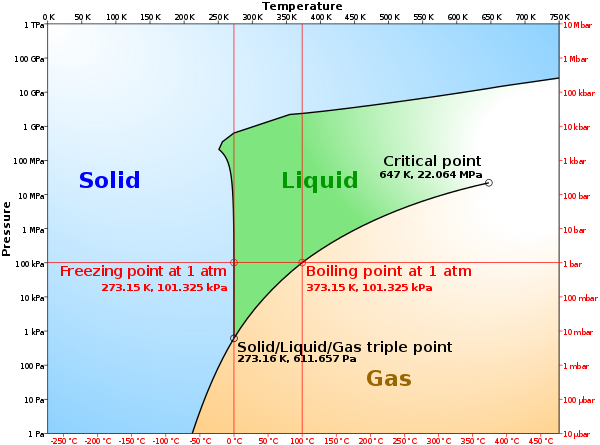
What happens if the temperature of a liquid is increased? The highest temperature at which a distinct liquid phase can exist is called the critical temperature, and the associated vapor pressure is called the critical pressure. These are the temperature and pressure at the Critical Point shown in Figure 2.10.
Solids can also evaporate just like liquids. However, in the case of solids, the process is called sublimation. The solid form of carbon dioxide, more commonly known as dry ice, is a familiar example. In dry ice, a crystalline solid, the molecules vibrate about their equilibrium position and undergo collisions with their nearest neighbors. This gives rise to a distribution of energies, similar to a liquid. At the surface of the solid, some of the molecules possess kinetic energies large enough to enable them to break away from the surface and enter the vapor phase. If this process occurs in a closed chamber, an equilibrium condition will occur when the rate at which molecules leave the solid equals the rate at which they return to the solid. The pressure exerted by the vapor is the equilibrium vapor pressure of the solid.
A commercial example that uses sublimation is freeze-drying. Freeze-dried instant coffee begins as a batch of brewed coffee. The brewed coffee is then frozen and the ice (water) component is removed under vacuum. In this way, the delicate heat-sensitive molecules are preserved and the flavor is retained.
Summary
Knowledge of the behavior of gases is useful in understanding the operation of vacuum systems. The kinetic theory of gases is an important model that describes the physical behavior of gases. Based on the assumption of this theory, we can predict and account for the following physical phenomena associated with gas behaviors:
- Gases will expand to uniformly fill the enclosure in which they are confined.
- Gases are compressible.
- Gases captured in a volume with elastic boundaries will cause the volume to expand/contract in response to temperature changes.
- Gases of equal volume and pressure have an equal number of molecules.
- The total pressure of a mixture of gases is equal to the sum of the partial pressures of each gas in the mixture.
Four physical variables define a gaseous system: pressure, temperature, volume, and the number of moles of gas. The ideal gas law is a mathematical model that relates these four parameters. We use this model to predict a physical state of the system if we can measure the other physical states.
There are other important physical phenomenon attributed to gases. Gases can move via the processes of diffusion and permeation. Gases can adsorb onto, absorb into, and desorb from surfaces. Gases can conduct thermal energy.
Molecules with enough energy can escape from the solid (sublimation) or liquid (evaporation) state as a vapor and enter into the gas load adjacent to the interface. These molecules that escape into the gas load contribute to the total gas pressure. The maximum amount of molecules that can escape into the gas load is determined by the vapor pressure of the solid or liquid. Vapor pressure is a function of temperature.
Gas pressure can be expressed with different units of measure. The vacuum regime includes gas pressures that are less than atmospheric pressure. Different gauge types are used to measure the pressure in a vacuum system. Absolute pressure values must be used to solve problems based on applications of the ideal gas law.
Chapter 2 Quiz
References
Brady, James E. General Chemistry: Principles & Structure. 5th ed., Hoboken, NJ: John Wiley, 1990.
LeMay, H. Eugene, Jr., et al. Chemistry: Connections to Our Changing World. Upper Saddle River, NJ: Prentice-Hall, Inc. 1996.
Mahan, J. E. Physical Vapor Deposition of Thin Films. Hoboken, NJ: John Wiley, 2000.
O’Hanlon, J.F. A User’s Guide to Vacuum Technology. 3rd ed., Hoboken, NJ: Wiley Interscience, 2003.
Tocci, S. and C. Viehland. Chemistry: Visualizing Matter. Fort Worth, TX: Holt, Rinehart & Winston, 1996.
Questions and Problems
- Using the concepts presented in this chapter, explain why:
- It is more difficult to open the freezer door just after you have opened and closed it a few moments before.
- A balloon filled with helium is buoyant one day, but it has less “lift” the next day.
- It is difficult to separate two plastic cups when one is stacked inside the other for more compact storage.
- A plastic water bottle emptied and capped off at cruising altitude during flight, collapses during the landing especially at a destination located at sea level.
- In our local newspaper the other day, the barometric pressure was given as 29.93 and falling. In what units is this barometric pressure reading given?
- A gas is compressed form a volume of 0.60 liter to 0.35 liter. If the initial pressure was 500 Torr, what is the final pressure? Assume that the temperature of the gas remains constant.
- At a temperature of 25°C and a pressure of 1 atm, a gas occupies a volume of 1.25 liters. If the temperature is increased to 75°C and the pressure remains constant at 1 atm, what is the new volume that the gas occupies?
- A bicycle pump has a barrel 65 cm long. On the up-stroke, air is drawn into the pump at a pressure of 1 atm. On the down-stroke, air in the barrel is compressed. How long must the down-stroke be to increase the pressure of the air in the barrel to 4 atm? Assume that the temperature of the air remains constant during the compression process.
- Calculate the number of liters occupied at STP by 0.35 moles of nitrogen gas (N2).
- A 2.0-liter mixture of gases is produced from 2.0 liters of O2 at 300 Torr, 2.0 liters of N2 at 500 Torr, and 2.0 liters of Ar at 100 Torr. What is the pressure of the mixture of gases in torr?
- Two chambers are connected by a U-shaped manometer. The manometer is filled with oil having a density of 0.910 g/mL. The pressure of the gas in Chamber A is 550 torr, and the oil in the arm of the manometer connected to Chamber A is 85 cm higher than the oil in the arm of the manometer connected to Chamber B. What is the pressure in Chamber B?
- You have been assigned the task of decorating a ballroom with 250 helium-filled balloons. A 25-liter helium tank filled with helium at a pressure of 25.0 atm and three 100-balloon packages have been delivered to the ballroom. If each balloon, when filled, holds 2.4 liters of helium at a pressure of 1.09 atm, will you be able to fill all 250 balloons? Assume the gas temperature stays constant as the balloons are filled.
- (a) What is the volume occupied by 2.00 mol of air at standard test conditions (1 atm and 0°C)? Treat air as ideal gas. (b) What is the number of molecules per cubic cm?
- 1000 cm3 of air at 40°C and pressure of 752 Torr expands until its volume is 1500 cm3 and its pressure is 644 Torr.
- Find the number of moles of air present.
- Find the final temperature of the sample in degrees Celsius.
- The best laboratory vacuum has a pressure of 1.00 x 10-18 atm. If the temperature in the room is 25°C, how many gas molecules are there per cubic centimeter?
- From Chemistry: Connections to our Changing World by H. Eugene LeMay, Jr., p. 430:
The Scene: The local county fair. A magician has just announced to a crowd of people at the fair that he can tell one gas apart from another just by feeling the gases. “You can’t feel a gas,” came a voice from the crowd. “Well,” said the magician, “for the price of my show, which happens to be one dollar, I’ll demonstrate that I can identify a gas by the way it feels. If I can do it successfully, I get to keep the money. But if I fail, you will get a refund. How’s that?
Their curiosity aroused, people quickly paid the money and within a very short time, the magician’s tent was full of eager spectators. They could not imagine how the magician would be able to tell two gases apart just by feel, without relying on color or odor. The magician stepped from behind a curtain holding two stoppered bottles. “Fill one bottle with xenon and the other with helium. Make sure you keep track of which gas is in which bottle.”
A volunteer from the crown filled the bottles from the compressed gas tanks that were conveniently secured to the stage. She identified each bottle with a secret mark and then gave the bottles to the magician.
The magician examined each bottle, took each stopper off briefly and stuck his finger into the bottles. “This is helium and this is xenon,” he said. He was right! He performed the trick several times and never failed. How did he do it?
- A recent advertisement appeared in a local newspaper about a local tire store filling car tires with pure nitrogen gas instead of atmospheric air. The advertisement claimed that tires filled with pure nitrogen gas leaked slower than tires filled with atmospheric air. Is this claim valid? Give a supporting argument or reason for your answer.

This work is supported by the National Science Foundation under grant number 2000454. Any opinions, findings, and conclusions or recommendations expressed in this e-book are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Media Attributions
- Figure 2.1. © Alexander Kramida, Karen Olsen, and Yuri Ralchenko is licensed under a Public Domain license
- Figure 2.2. © MATEC is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Figure 2.3. © Gigi Bocek is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Figure 2.4. © Fouad A. Saad/Shutterstock.com
- Figure 2.5. © E. Brewer is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Figure 2.6. © E. Brewer is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Figure 2.7. © Gigi Bocek is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Private: Animation 2.3. Diffusion Animation © Kurt J. Lesker Company is licensed under a CC BY-ND (Attribution NoDerivatives) license
- Private: Animation 2.3. Permeation animation © Kurt J. Lesker Company is licensed under a CC BY-ND (Attribution NoDerivatives) license
- Figure 2.8. © tersetki
- Figure 2.9. © Yannick Trottier is licensed under a CC BY (Attribution) license
- Figure 2.10. © Cmglee is licensed under a CC BY-SA (Attribution ShareAlike) license
Generally referring to the condition when gas-phase molecules have adsorbed onto a surface or coalesced within a volume to an extent that this can be visually observed.
Transition of a substance directly from a solid state/phase to a gas state/phase.
Pressure defined in 1925 by the National Advisory Committee for Aeronautics as 760 Torr (101,325 Pascal, or 1013.25 mBar, or 29.9213 inches of Hg) for a “normal” day at 0°C and at sea level.
The taking up of a gas or vapor by a solid or liquid due to physical forces in which the gas is retained at the surface of the solid or the liquid. Adsorbed gases are not bound to a surface permanently.
The transition of a liquid to a solid by the removal of heat, i.e. lowering the temperature of the liquid. An example is water, a liquid at room temperature, when it turns to ice as the temperature is lowered below its freezing point.
The term “vapor” is often used when a material may be present in several phases within a vacuum chamber at a given pressure. For example, during thermal evaporation of a metal, metal generally exists as a solid source, then as a pool of liquid metal as the temperature increases, and finally as a metal vapor evaporating from the surface of the liquid. The evaporated metal vapor will re-condense into a solid when it adsorbs onto any relatively cool surface (i.e., a substrate).
A process where surface-bound molecules are thermally desorbed from a solid or liquid surface to become part of the gas phase. Evaporation typically takes place below the boiling temperature.
The sealed part(s) of pressure-controlled research or production apparatus where vacuum and/or other processes occur.
A way of measuring how much force is acting over an area or the perpendicular force per unit area.
A pressure unit defined as Pounds per Square Inch (of Gas).
The difference between absolute pressure and atmospheric pressure.
The total pressure measured with reference to absolute zero pressure, that is, the condition of perfect vacuum. The following values correspond to absolute zero pressure: 0 Pa = 0 Torr = 0 mbar.
Widely used (but non-SI) pressure unit in vacuum technology, equal to 1 mm of mercury in a historic barometer, and named after Italian physicist Evangelista Torricelli (1608-1647). Torr is still widely used in the US, and is therefore the pressure unit primarily used in this e-book.
The bar is a metric unit of pressure but is not part of the International System of Units (SI). One bar is exactly equal to 100,000 Pa. The millibar (mbar) is a unit of pressure typically used to express vacuum pressures. One mbar is exactly equal to 100 Pa.
The SI unit of pressure equal to one newton per square meter. There are 101,325 pascals in one standard atmosphere. There are 1,000 Pa in 1 kPa. Named after French mathematician and philosopher, Blaise Pascal (1623-1662).
International System of Units (Abbreviation of French: Systeme International d’unites). The only system of measurement with official status in nearly every country in the world.
One of several types of electrical or mechanical devices used to measure pressure and/or gas density at various locations of a vacuum system.
Vacuum pressure regime with pressures between 760 Torr and 1E-3 Torr.
Pressure gauges that operate by sensing deflection of a solid or liquid surface caused by momentum transfer to that surface from energetic gas molecules. Direct reading gauges are largely insensitive to gas type.
A type of direct reading vacuum gauge with a thin-walled metal tube bent into a circular arc that will straighten if pressure is applied to the inside of the tube. The movement of the metal tube is used to indicate pressure. Bourdon gauge was invented by Eugene Bourdon (1808-1884), a brilliant French watchmaker and engineer, in 1849.
A manometer-type and direct reading rough vacuum gauge that measures the displacement of a thin solid membrane caused by pressure difference on opposite sides of the membrane.
Pressure gauges that measure a property related to gas pressure and then convert that measurement into a gas pressure reading.
An individual particle in a vacuum that has neither a defined volume or shape. A gas molecule can be a single atom (e.g., a noble gas such as Argon, Ar) or a number of atoms bonded together to form a compound (e.g., such as water).
The pressure exerted by a particular species of gas molecules. According to Dalton’s law, the sum of the partial pressures of all the component species in a mixture is equal to the total pressure.
The number of molecules per unit volume of gas.
A measure of the instantaneous relative volume change of a fluid or solid as a response to a pressure change.
Gas law that states that if the temperature and the amount of gas are held constant, the volume of gas is inversely proportional to the pressure exerted by the gas.
Gas law that states that the volume of a gas is directly proportional to the absolute temperature at a constant pressure. Also known as the law of volumes.
Gas law that describes how the absolute pressure of a gas depends on its temperature while the volume of the gas is held constant. Also known as Amonton’s law.
In vacuum technology, defined as a temperature of 273 K (0 degree C) and an absolute pressure of exactly one standard atmosphere (1 atm, 760 Torr, or 101.325 kPa at sea level). Since 1982, Defined by IUPAC (International Union of Pure and Applied Chemistry) as a temperature of 273 K (0 degree Celsius) and an absolute pressure of exactly 105 Pa (100 kPa, 1 bar).
The total pressure is equal to the sum of the partial pressures of each gas in the mixture.
See ideal gas constant.
The average distance which a molecule travels between two successive collisions with other molecules of the gas.
The liberation of gases and vapors sorbed (adsorbed and absorbed) by a material.
A structural state of matter in which the thermal motion of the respective molecule species near room temperature is sufficient to exceed any cohesive forces, and permit their free motion. Contrast with term vapor phase.
Molecules that have a hydrogen bonded to nitrogen, oxygen, or fluorine have unusually strong dipole-dipole attractions called hydrogen bonds.
The amount of gas that must be removed from the chamber in a vacuum system by the vacuum pump(s). It is typically measured in torr-liters per second, cubic feet per minute, or cubic meters per hour.
Any one of the many parts that are required to construct a functioning vacuum system, or parts required to undertake and control a vacuum process.
A process in which atoms or molecules move through a solid, liquid or gas.
The process of molecular penetration of gases, vapors, or fluids completely through a material.
The pressure exerted by a vapor in thermodynamic equilibrium with its condensed phases (solid or liquid) at a given temperature in a closed system.

