Suggested Pre-lab Assignment

1. Predict the pump-down time and the shape of the pump-down curve for the system assuming no outgassing sources are present.
2. Predict how the pump-down curve, envisioned in Question 1, will change with the addition of a ½” x ½” piece of dry paper towel as an added outgassing source in the chamber.
3. Predict how the pumpdown curve, envisioned in Question 2, will change with a small amount of water added to the piece of paper towel in Question 2.

Theoretical Background

As a rough vacuum pump removes gas from the chamber, the chamber pressure drops non-linearly as shown in the Figure 7.1 below. According to Boyle’s law, the pressure in the chamber after each stroke/cycle of the rough vacuum pump can be calculated as:

[latex]\begin{equation} P_{after \thinspace 1 \thinspace stroke} = P_{initial} \frac {V_{initial}}{V_{after \thinspace 1 \thinspace stroke}} \end{equation}[/latex]

where

P_initial = pressure before stroke,

V_initial = volume of the process chamber, and

V_{after 1 stroke} = volume of the process chamber + vacuum pump’s expansion volume.

The volume after 1 stroke is larger than the initial volume because the gas in the process chamber expands to occupy the volume of the process chamber plus the volume of the vacuum pump’s expansion volume. As Boyle’s law suggests, the gas pressure in the process chamber and throughout the expanded space decreases. At the end of the stroke, the pump isolates the expansion volume from the process chamber volume, compresses the trapped gas and exhausts it to atmosphere. However, the pressure in the chamber volume retains its lower pressure condition. At the beginning of the next stroke the initial pressure within the chamber starts from this lower pressure condition. In this way, each iteration of the pump’s stroke cycle reduces the gas pressure within the process chamber.

Each consecutive pumping cycle achieves a smaller and smaller pressure reduction in the process chamber. After N strokes/cycles, this non-linear reduction in pressure over time can be estimated as:

[latex]\begin{equation} P_{after \thinspace N \thinspace strokes} = P_{initial} \left( \frac {V_{initial}}{V_{after \thinspace 1 \thinspace stroke}} \right)^N \end{equation}[/latex]

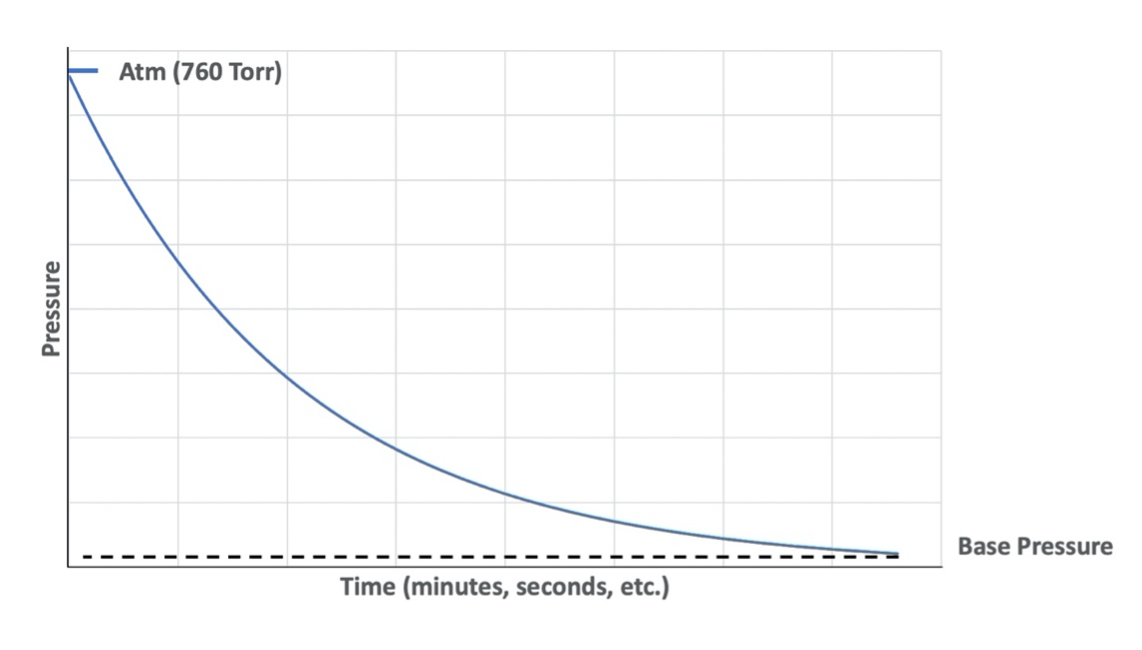
When sources of outgassing are present in the vacuum system, those outgassing sources add to the gas load within the system. Since the vacuum system must also remove any gas molecules present associated with outgassing sources, the presence of outgassing sources in a vacuum system will affect the pump-down time and the shape of the pump-down curve. Generally, it takes longer to pump down to a target vacuum pressure when outgassing sources are present. If the gas load from outgassing is substantial, the vacuum system may not be able to reach the target pressure. This phenomenon can be observed on the pump-down curve as a pressure plateau that corresponds to the vapor pressure of the outgassing source. If the gas load generated from the outgassing source can be reduced by the system, the vacuum system should attain its standard operating pump-down time performance with a corresponding pump-down curve showing no indications of the outgassing source.

Equipment and Materials

1. Vacuum system consisting minimally of: (one each of the following components)
   1. Process chamber
   2. Absolute pressure measurement device(s)
   3. Vent valve
   4. Isolation/roughing valve
   5. Vacuum piping
   6. Rough vacuum pump
2. Timer
3. Barometer (not necessary if the vacuum system includes an absolute pressure measurement device with a measurement range that includes atmospheric pressure)
4. Manufacturer’s specifications for the rough vacuum pump including the pump’s ultimate pressure and the pumping speed chart
5. 2, ½” x ½” paper towel squares
6. Beaker
7. Water

Procedure

Learning Activity 7.1: Baseline Vacuum Pump-Down Cycle

1. Power the absolute pressure measurement gauge(s) (Pirani gauge, convection-enhanced Pirani gauge, and/or capacitance diaphragm gauge). Allow the electronic gauge(s) to warm up.
2. Identify the ultimate pressure of the rough vacuum pump from the pump manufacturer’s specifications.
3. Open the vent valve and vent the process chamber to atmosphere.
4. Identify and record current atmospheric pressure using a barometer or an absolute gauge on the vacuum system.
5. Close the vent valve and roughing valve.
6. Start the rough vacuum pump and run for few seconds.
7. Open the roughing valve and start the timer at the same time.
8. Record pressure measurements from the pressure measuring device every 5 to 10 seconds for 2 to 5 minutes in Table 7.1, until the pressure stops decreasing for more than 20 seconds or when pump’s ultimate pressure is approached.
9. Close roughing valve.
10. Turn off the rough vacuum pump.