Learning Activity 1.1: Marshmallow Preparation – Measurements and Calculations
- Measuring the dimensions and mass of a cylindrically-shaped object, such as marshmallow.
- Making calculations of surface area, volume, and density of the cylindrically-shaped object.
- Measure linear dimensions and the mass of a cylindrical object using proper techniques.
- Calculate surface area and volume of a cylindrical object.
- Calculate density of an object.
- Report final calculated results with the correct number of significant digits.
Suggested Pre-lab Assignment
-
Find 3 measuring instruments at your home or workplace and identify units of measurement and the smallest division of the measurement. Examples: bathroom scale, kitchen scale, tape measure, measuring cup, timer, etc.
Instrument
Unit
Smallest Division
Report the following results with the appropriate number of significant figures.
-
Convert 45.3 mm (millimeters) to units of cm (centimeters).
Convert 45.3 mm to units of meters.
Calculate the volume of a cube that is 2.0 cm x 2.0 cm x 2.0 cm.
Calculate the surface area of a cube that is 2.0 cm x 2.0 cm x 2.0 cm.
Theoretical Background
Figure 1.1 shows a cylindrically-shaped object with its diameter D and height H indicated on the figure.

The surface area of the flat top or bottom part of the cylinder can be calculated using Equation 1.1:
[latex]\begin{equation} A_{circle} = \frac {\pi D^2}{4} \qquad \qquad \qquad (Eq. 1.1) \end{equation}[/latex]
It can also be calculated using radius R = D/2:
[latex]\begin{equation} A_{circle} = \pi R^2 \end{equation}[/latex]
The surface area of the wall (tube) can be calculated using Equation 1.2:
[latex]\begin{equation} A_{tube} = \pi DH \qquad \qquad \qquad (Eq. 1.2) \end{equation}[/latex]
or, alternatively, using radius instead of diameter as:
[latex]\begin{equation} A_{tube} = 2 \pi RH \end{equation}[/latex]
Then the total surface area (Figure 1.2) can be determined by adding the areas of both the top and bottom circle and the surface area of the tube as shown in Equation 1.3:
[latex]\begin{equation} A_{surface} = 2A_{circle} + A_{tube} \qquad \qquad \qquad (Eq. 1.3) \end{equation}[/latex]
Surface area of the tube is equal to the area of the rectangle as shown in Figure 1.2.
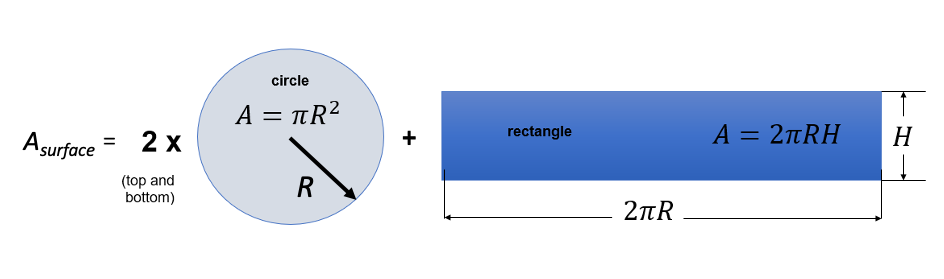
Then, volume of the cylinder can be determined using Equation 1.4:
[latex]\begin{equation} V = A_{circle} H = \left( \frac {\pi D^2}{4} \right)H \qquad \qquad \qquad (Eq. 1.4) \end{equation}[/latex]
When measuring the height or diameter of the cylinder, different measuring tools can be used. The resolution of the measuring tool dictates the number of significant digits for the measured quantity. If the measured values for the diameter and height have different numbers of significant digits, then how many significant digits should be present in the final answer for a calculated value, such as volume? The final answer should contain the same number of significant digits as the measured quantity with the least number of significant digits used in the calculation, for example, the diameter or height parameter.
As an example, if H = 15.0 cm and D = 2.0 cm, then the height value has 3 significant digits while the diameter value has only 2 significant digits. This means that the calculated value for volume should be rounded to 2 significant digits:
[latex]\begin{equation} V = \left( \frac {\pi (2.0cm)^2}{4} \right)(15.0cm) = 47.12389 \thinspace cm^3. \end{equation}[/latex]
So, the calculated result yields a value of 47.12389 cm3. When the rules of significant figures are applied, the final result will be reported as 47 cm3. If the third digit had been greater than or equal to 5, for example 47.62389, then the second digit would be rounded up to an 8 for a final result of 48 cm3. Note that only the final answer reported should be rounded to the correct number of significant digits. If you are using the calculated volume to calculate another quantity, you should include the resolution of the calculated value, that is, 47.12389 cm3 to reduce rounding error.
Another useful quantity which can be determined for any object is its volume density or density. Density ρ is determined by dividing the mass of the object M by its volume V as shown in Equation 1.5:
[latex]\begin{equation} ρ = \frac {M}{V} \qquad \qquad \qquad (Eq. 1.5) \end{equation}[/latex]
with units being unit of mass divided by unit of volume. If mass is measured in grams (g) and volume is calculated in cm3, then the density will have units of g/cm3. Note, when the object expands, it will occupy a larger volume. Dividing the same mass by a larger volume yields a smaller density. Alternatively, when the volume becomes smaller, the density increases.
Equipment and Materials
- 1 Ruler with units of measure in millimeters (mm)
- 1 Mass Scale or Mass Balance with units of measure in grams (g)
- Sharpie pen
- 2 Marshmallows (Jumbo size if available)
- Plastic Ziploc bag to store marshmallows for another Learning Activity
Procedure
- Use a sharpie or felt tip pen to mark one marshmallow with a 1 and the other marshmallow with a 2.
- Identify measurement tools and measurement resolution:
Tool 1
Tool 1 unit of measure
Tool 1 resolution
Tool 2
Tool 2 unit of measure
Tool 2 resolution
Use a ruler displaying units of measure in millimeters (mm) and centimeters (cm) to measure the diameter and height of Marshmallow "1". If the flat surface face of the marshmallow has an obvious oval shape rather than a near circle shape, measure the long diameter and the short diameter and calculate the average of the two diameters.
| Diameter D (centimeters, cm) |
|
| Height H (centimeters, cm) |
Calculate volume V (cubic centimeters (cc or cm3)):
Calculate surface area of the flat bottom (circle) (square centimeters (cm2)):
Calculate surface area of the wall (tube) (square centimeters (cm2)):
Calculate total surface area (square centimeters (cm2)):
Use a scale that displays units of measure in grams (g) to measure the mass M of the marshmallow:
| Mass M (grams, g) |
|---|
Calculate density ρ (gram/cubic centimeter, g/cm3, or g/cc):
Significant Figures: report all calculated values with the appropriate significant figures:
| Volume |
|
| Surface area of the bottom face (circle) |
|
| Surface area of the wall (tube) |
|
| Total surface area |
|
| Density |
Take measurements for the second marshmallow and record all relevant quantities below:
| Diameter D (centimeters, cm) |
|
| Height H (centimeters, cm) |
|
| Mass M (grams, g) |
Place Marshmallow "1" and Marshmallow "2" in Ziploc bag and seal it tightly. Write your group member’s name on the bag. We will use the marshmallows for the next week’s activity with the Rough Vacuum Equipment Trainer.
After class, repeat the calculations we did in class, but this time for Marshmallow "2".
- Calculate the volume V of marshmallow "2" in units of cm3 and report with appropriate significant figures:
- Calculate the surface area for the flat bottom (circle) in units of cm2 and report with appropriate significant figures:
- Calculate the surface area for the wall (tube) in units of cm2 and report with appropriate significant figures:
- Calculate the total surface area in units of cm2 and report with appropriate significant figures:
- Calculate the density of Marshmallow "2" in units of g/cm3 (or g/cc, or gram/cubic centimeter) and report with appropriate significant figures:
- Report all calculated values with the appropriate significant figures:
Volume
Surface area of the bottom face (circle)
Surface area of the wall (tube)
Total surface area
Density

This work is supported by the National Science Foundation under grant number ATE DUE 2000454. Any opinions, findings, and conclusions or recommendations expressed in this e-book are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Media Attributions
- Figure 1.1. is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Figure 1.2. is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license

